
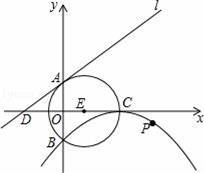
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=
 x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.

【考点】二次函数综合题.
【专题】压轴题.
【分析】(1)连接AE,由已知得:AE=CE=5,OE=3,利用勾股定理求出OA的长,结合垂径定理求出OC的长,从而得到C点坐标,进而得到抛物线的解析式;
(2)求出点D的坐标为(﹣
 ,0),根据△AOE∽△DOA,求出∠DAE=90°,判断出直线l与⊙E相切与A.
,0),根据△AOE∽△DOA,求出∠DAE=90°,判断出直线l与⊙E相切与A.
(3)过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.设M(m,
 m+4),P(m,﹣
m+4),P(m,﹣
 m2+m﹣4),得到PM=
m2+m﹣4),得到PM=
 m+4﹣(﹣
m+4﹣(﹣
 m2+m﹣4)=
m2+m﹣4)=
 m2﹣
m2﹣
 m+8=
m+8=
 (m﹣2)2+
(m﹣2)2+
 ,根据△PQM的三个内角固定不变,得到PQ最小=PM最小•sin∠QMP=PM最小•sin∠AEO=
,根据△PQM的三个内角固定不变,得到PQ最小=PM最小•sin∠QMP=PM最小•sin∠AEO=
 ×
×
 =
=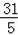
 ,从而得到最小距离.
,从而得到最小距离.
【解答】解:(1)如图1,连接AE,由已知得:AE=CE=5,OE=3,
在Rt△AOE中,由勾股定理得,OA=
 =
=
 =4,
=4,
∵OC⊥AB,
∴由垂径定理得,OB=OA=4,
OC=OE+CE=3+5=8,
∴A(0,4),B(0,﹣4),C(8,0),
∵抛物线的顶点为C,
∴设抛物线的解析式为y=a(x﹣8)2,
将点B的坐标代入上解析的式,得64a=﹣4,故a=﹣
 ,
,
∴y=﹣
 (x﹣8)2,
(x﹣8)2,
∴y=﹣
 x2+x﹣4为所求抛物线的解析式,
x2+x﹣4为所求抛物线的解析式,
(2)在直线l的解析式y=
 x+4中,令y=0,得
x+4中,令y=0,得
 x+4=0,解得x=﹣
x+4=0,解得x=﹣
 ,
,
∴点D的坐标为(﹣
 ,0),
,0),
当x=0时,y=4,
∴点A在直线l上,
在Rt△AOE和Rt△DOA中,
∵
 =
=
 ,
,
 =
=
 ,
,
∴
 =
=
 ,
,
∵∠AOE=∠DOA=90°,
∴△AOE∽△DOA,
∴∠AEO=∠DAO,
∵∠AEO+∠EAO=90°,
∴∠DAO+∠EAO=90°,即∠DAE=90°,因此,直线l与⊙E相切与A.
(3)如图2,过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.
设M(m,
 m+4),P(m,﹣
m+4),P(m,﹣
 m2+m﹣4),则
m2+m﹣4),则
PM=
 m+4﹣(﹣
m+4﹣(﹣
 m2+m﹣4)=
m2+m﹣4)=
 m2﹣
m2﹣
 m+8=
m+8=
 (m﹣2)2+
(m﹣2)2+
 ,
,
当m=2时,PM取得最小值
 ,
,
此时,P(2,﹣
 ),
),
对于△PQM,
∵PM⊥x轴,
∴∠QMP=∠DAO=∠AEO,
又∠PQM=90°,
∴△PQM的三个内角固定不变,
∴在动点P运动的过程中,△PQM的三边的比例关系不变,
∴当PM取得最小值时,PQ也取得最小值,
PQ最小=PM最小•sin∠QMP=PM最小•sin∠AEO=
 ×
×
 =
=
 ,
,
∴当抛物线上的动点P的坐标为(2,﹣
 )时,点P到直线l的距离最小,其最小距离为
)时,点P到直线l的距离最小,其最小距离为
 .
.




【点评】本题考查了二次函数综合题,涉及勾股定理、待定系数法求二次函数解析式、切线的判定和性质、二次函数的最值等知识,在解答(3)时要注意点P、点M坐标的设法,以便利用二次函数的最值求解.


科目:初中数学 来源: 题型:
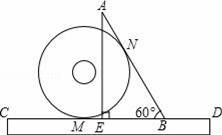
小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,甲、乙、丙图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
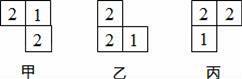

A.仅有甲和乙相同 B.仅有甲和丙相同
C.仅有乙和丙相同 D.甲、乙、丙都相同
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
如果单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项.求
(1)(7a﹣22)2013的值;
(2)若5mxay﹣5nx2a﹣3y=0,且xy≠0,求(5m﹣5n)2014的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年十一国庆长假提前到9月29日,黄金周期间外出旅游更为火爆,若旅游区的门票为60元/张,某旅游区的开放时间为每天10小时,并每小时对进入旅游区的游客人数进行一次统计,下表是9月30日对进入旅游区人数的7次抽样统计数据:
| 记数的次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
| 每小时进入旅游区的人数 | 318 | 310 | 310 | 286 | 280 | 312 | 284 |
那么从9月29日至10月5日旅游区门票收入是多少?( )
A.900000元 B.129600元 C.191600元 D.162000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com