
如果单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项.求
(1)(7a﹣22)2013的值;
(2)若5mxay﹣5nx2a﹣3y=0,且xy≠0,求(5m﹣5n)2014的值.
【考点】同类项.
【分析】(1)根据同类项是字母相同且相同字母的指数也相同,可得关于a的方程,解方程,可得答案;
(2)根据合并同类项,系数相加字母部分不变,可得m、n的关系,根据0的任何整数次幂都得零,可得答案.
【解答】解:(1)由单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项,得
a=2a﹣3,
解得a=3,
(7a﹣22)2013=(7×3﹣22)2013=(﹣1)2013=﹣1;
(2)由5mxay﹣5nx2a﹣3y=0,且xy≠0,得
5m﹣5n=0,
解得m=n,
(5m﹣5n)2014=02014=0.
【点评】本题考查了同类项,利用了同类项的定义,负数的奇数次幂是负数,零的任何正数次幂都得零.


科目:初中数学 来源: 题型:
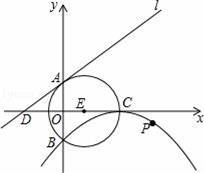
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=
 x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
2001年亚洲铁人三项赛在徐州市风光秀丽的云龙湖畔举行.比赛程序是:运动员先同时下水游泳1.5千米到第一换项点,在第一换项点整理服装后,接着骑自行车行40千米到第二换项点,再跑步10千米到终点.下表是2001年亚洲铁人三项赛女子组(19岁以下)三名运动员在比赛中的成绩(游泳成绩即游泳所用时间,其它类推,表内时间单位为秒)
| 运动员号码 | 游泳成绩 | 第一换项点所用时间 | 自行车成绩 | 第二换项点所用时间 | 长跑成绩 |
| 191 | 1997 | 75 | 4927 | 40 | 3220 |
| 194 | 1503 | 110 | 5686 | 57 | 3652 |
| 195 | 1354 | 74 | 5351 | 44 | 3195 |
(1)填空(精确到0.01):
第191号运动员骑自行车的平均速度是 米/秒;
第194号运动员骑自行车的平均速度是 米/秒;
第195号运动员骑自行车的平均速度是 米/秒;
(2)如果运动员骑自行车都是匀速的,那么在骑自行车的途中,191号运动员会追上195号或194号吗?如果会,那么追上时离第一换项点有多少米(精确到0.01)?如果不会,为什么?
(3)如果长跑也都是匀速的,那么在长跑途中这三名运动员中有可能某人追上某人吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线y=x2﹣(4m+1)x+2m﹣1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,
 )的下方,那么m的取值范围是( )
)的下方,那么m的取值范围是( )
A.
 B.
B.
 C.
C.
 D.全体实数
D.全体实数
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标分别为A(2,0),B(4,0),C(0,5),点D在第一象限内,且∠ADB=45°.线段CD的长的最小值为
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,﹣1),B(3,﹣1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.
(1)求经过O、A、B三点的抛物线的解析式;
(2)如果将△OPQ绕着点P按逆时针方向旋转90°,是否存在t,使得△OPQ的顶点O或顶点Q在抛物线上?若存在,请求出t的值;若不存在,请说明理由;
(3)求出S与t的函数关系式.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com