
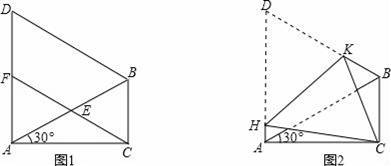
如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:①△AEF≌△BEC;②四边形BCFD是平行四边形;
(2)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,求sin∠ACH的值.


【考点】等边三角形的性质;全等三角形的判定;平行四边形的判定;翻折变换(折叠问题);解直角三角形.菁优网版权所有
【专题】综合题;压轴题.
【分析】(1)①在△ABC中,由已知可得∠ABC=60°,从而推得∠BAD=∠ABC=60°.由E为AB的中点,得到AE=BE.又因为∠AEF=∠BEC,所以△AEF≌△BEC.
②在Rt△ABC中,E为AB的中点,则CE=
 AB,BE=
AB,BE=
 AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.
AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.
(2)在Rt△ABC中,设BC=a,则AB=2BC=2a,AD=AB=2a.设AH=x,则HC=HD=AD﹣AH=2a﹣x.在Rt△ABC中,由勾股定理得AC2=3a2.
在Rt△ACH中,由勾股定理得AH2+AC2=HC2,即x2+3a2=(2a﹣x)2.解得x=
 a,即AH=
a,即AH=
 a.求得HC的值后,利用sin∠ACH=AH:HC求值.
a.求得HC的值后,利用sin∠ACH=AH:HC求值.
【解答】(1)证明:①在△ABC中,∠ACB=90°,∠CAB=30°,
∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,
∴∠BAD=∠ABC=60°.
∵E为AB的中点,
∴AE=BE.
又∵∠AEF=∠BEC,
∴△AEF≌△BEC.
②在△ABC中,∠ACB=90°,E为AB的中点,
∴CE=
 AB,BE=
AB,BE=
 AB.
AB.
∴CE=AE,
∴∠EAC=∠ECA=30°,
∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,
∴∠AFE=∠BCE=60°.
又∵∠D=60°,
∴∠AFE=∠D=60°.
∴FC∥BD.
又∵∠BAD=∠ABC=60°,
∴AD∥BC,即FD∥BC.
∴四边形BCFD是平行四边形.
(2)解:∵∠BAD=60°,∠CAB=30°,
∴∠CAH=90°.
在Rt△ABC中,∠CAB=30°,设BC=a,
∴AB=2BC=2a.
∴AD=AB=2a.
设AH=x,则HC=HD=AD﹣AH=2a﹣x,
在Rt△ABC中,AC2=(2a)2﹣a2=3a2,
在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a﹣x)2,
解得x=
 a,即AH=
a,即AH=
 a.
a.
∴HC=2a﹣x=2a﹣
 a=
a=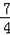
 a.
a.
∴sin∠ACH=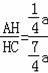
 =
=
 .
.

【点评】本题考查了:
(1)折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
(2)全等三角形的判定和性质,等腰直角三角形的性质,勾股定理,平行线的判定和性质,平行四边形的判定和性质,正弦的概念求解.


科目:初中数学 来源: 题型:
2015年十一国庆长假提前到9月29日,黄金周期间外出旅游更为火爆,若旅游区的门票为60元/张,某旅游区的开放时间为每天10小时,并每小时对进入旅游区的游客人数进行一次统计,下表是9月30日对进入旅游区人数的7次抽样统计数据:
| 记数的次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
| 每小时进入旅游区的人数 | 318 | 310 | 310 | 286 | 280 | 312 | 284 |
那么从9月29日至10月5日旅游区门票收入是多少?( )
A.900000元 B.129600元 C.191600元 D.162000元
查看答案和解析>>
科目:初中数学 来源: 题型:
反比例函数y=
 的图象如图所示,以下结论正确的是( )
的图象如图所示,以下结论正确的是( )
①常数m<1;
②y随x的增大而减小;
③若A为x轴上一点,B为反比例函数上一点,则S△ABC=
 ;
;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.


A.①②③ B.①③④ C.①②③④ D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
平面直角坐标系xOy中,点A、B分别在函数y1=
 (x>0)与y2=﹣
(x>0)与y2=﹣
 (x<0)的图象上,A、B的横坐标分别为
(x<0)的图象上,A、B的横坐标分别为
a、b.


(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;
(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=
 (x>0)的图象都有交点,请说明理由.
(x>0)的图象都有交点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com