
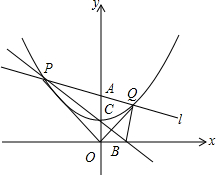
 如图,在直角坐标系中,直线l是绕着定点A(0,2)旋转的动直线,且与经过点C(0,1)的抛物线y=$\frac{1}{4}{x}^{2}+h$交于不同的两点P和Q(即直线l在旋转过程中,不与y轴平行).
如图,在直角坐标系中,直线l是绕着定点A(0,2)旋转的动直线,且与经过点C(0,1)的抛物线y=$\frac{1}{4}{x}^{2}+h$交于不同的两点P和Q(即直线l在旋转过程中,不与y轴平行).分析 (1)将(0,1)代入抛物线的解析式即可求得h的值;
(2)当PQ∥x轴时,△PQ0的面积最小,将y=0代入抛物线的解析式可求得Q、P的坐标,从而可求得PQ的长,最后依据三角形的面积公式求解即可;
(3)设P(a,$\frac{1}{4}$a2+1),然后求得直线QA、PC的解析式(含字母a),然后再求得点B、Q的坐标,从而可作出判断.
解答 解:(1)将(0,1)代入y=$\frac{1}{4}{x}^{2}+h$得:h=1.
(2)∵h=1,
∴y=$\frac{1}{4}$x2+1.
观察函数图象可知:当PQ∥x轴时,△PQ0的面积最小.
∵将y=2代入抛物线的解析式得:$\frac{1}{4}$x2+1=2,解得x1=2,x2=-2,
∴PQ=4.
∴S△PQO=$\frac{1}{2}×4×2$=4.
(3)设P(a,$\frac{1}{4}$a2+1)其中a≠0,直线AP的解析式为y=kx+2,直线PC的解析式为y1=k1x+1.
∵将点P的坐标代入得;ak+2=$\frac{1}{4}$a2+1,ak1x+1=$\frac{1}{4}$a2+1,解得:k=$\frac{a}{4}-\frac{1}{a}$,k1=$\frac{a}{4}$,
∴直线AP的解析式为y=($\frac{a}{4}-\frac{1}{a}$)x+2,PC的解析式为y=$\frac{a}{4}$x+1.
∵令y1=0得:$\frac{a}{4}$x+1=0,解得;x=-$\frac{4}{a}$,
∴B(-$\frac{4}{a}$,0).
将y=($\frac{a}{4}-\frac{1}{a}$)x+2与y=$\frac{1}{4}$x2+1联立得:$\frac{1}{4}$x2+1=($\frac{a}{4}-\frac{1}{a}$)x+2,整理得:$\frac{1}{4}$x2-($\frac{a}{4}-\frac{1}{a}$)x-1=0,
∵a是方程$\frac{1}{4}$x2-($\frac{a}{4}-\frac{1}{a}$)x-1=0的一个实根,
∴ax2=-4.
∴x2=-$\frac{4}{a}$.
∴点Q的横坐标相同.
∴QB∥AO.
当a≠±2时,QB≠AO,此时四边形AOBQ是直角梯形.
当a=±2时,QB=AO.
∵QB=AO,QB∥AO,
∴四边形AOBQ是平行四边形.
又∵∠AOB=90°,
∴四边形AOBQ是正方形.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,三角形的面积公式、梯形的判定、正方形的判定,一元二次方程根与系数的关系,求得点B与点Q的横坐标(用含a的式子表示)是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
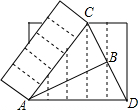 两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.
两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
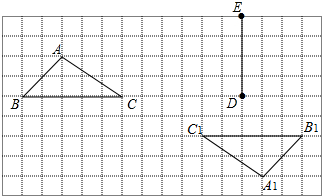 在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心对称图形.
在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心对称图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com