Question

【题目】如图，已知AB是⊙O的直径，点P为圆上一点，点C为AB延长线上一点，PA=PC，∠C=30°．

（1）求证：CP是⊙O的切线．
（2）若⊙O的直径为8，求阴影部分的面积．

Answer 1

【答案】
（1）证明：连接OP，如图所示：

∵PA=PC，∠C=30°，

∴∠A=∠C=30°，

∴∠APC=120°，

∵OA=OP，

∴∠OPA=∠A=30°，

∴∠OPC=120°﹣30°=90°，

即OP⊥CP，

∴CP是⊙O的切线．

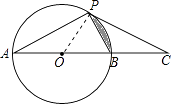
（2）解：∵AB是⊙O的直径，

∴∠APB=90°，

∴∠OBP=90°﹣∠A=60°，

∵OP=OB=4，

∴△OBP是等边三角形，

∴阴影部分的面积=扇形OBP的面积﹣△OBP的面积= ﹣ ×4×2 = ﹣4 ．

【解析】（1）连接OP，由等腰三角形的性质得出∠C=∠OPA=30°，∠APC=120°，求出∠OPC=90°即可；（2）证明△OBP是等边三角形，阴影部分的面积=扇形OBP的面积﹣△OBP的面积，即可得出结果．本题考查的是切线的判定、等腰三角形的性质、圆周角定理、等边三角形的判定与性质、扇形面积公式等知识；熟练掌握切线的判定．证明三角形是等边三角形是解决问题（2）的关键．