Question

16．在正方形ABCD中，点E为BC边上一点，连接AE．以AE为一边作∠EAF=45°，AF交直线BC于点F．连接DF．若AB=6．BE=2．则线段DF的长为6$\sqrt{2}$或3$\sqrt{13}$．

Answer 1

分析 根据AF的不确定，分两种情况：
①当AF在AE的右侧时，如图1，证明△ABH≌△ADG和△AHE≌△AGE，得EG=EH，设DG=x，在Rt△ECG中，利用勾股定理列方程解出即可，最后再利用勾股定理求DF的长；
②当AF在AE的左侧时，如图2，设BF=x，同理可求出x的值，同理可利用勾股定理求DF的长．

解答 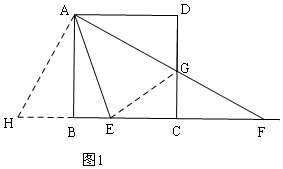解：分两种情况：
①当AF在AE的右侧时，如图1，
延长CB至H，使BH=DG，连接AH，
∵四边形ABCD为正方形，
∴AB=AD，∠ABC=∠ADC=90°，
∴∠ABH=∠ADC=90°，
∴△ABH≌△ADG，
∴∠HAB=∠GAD，AG=AH，
∵∠EAF=45°，∠BAD=90°，
∴∠BAE+∠GAD=∠BAE+∠HAB=45°，
即∠HAE=45°，
∴∠HAE=∠EAF，
∵AE=AE，
∴△AHE≌△AGE，
∴EG=EH，
设DG=x，则CG=6-x，EG=EH=2+x，
∵BC=6，BE=2，
∴EC=4，
由勾股定理得：（2+x）²=（6-x）²+4²，
x=3，
∴CG=6-x=6-3=3，
∵四边形ABCD为正方形，
∴CG∥AB，
∴△GCF∽△ABF，
∴$\frac{GC}{AB}=\frac{CF}{BF}$，
∴$\frac{3}{6}$=$\frac{CF}{CF+6}$，
∴CF=6
在Rt△DCF中，由勾股定理得：DF=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$，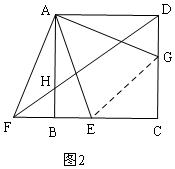
②当AF在AE的左侧时，如图2，
设BF=x，
在DC上截取DG=BF=x，连接AG、EG，
则CG=6-x，
同理得：△AEF≌△AEG，
∴EG=EF=2+x，
在Rt△ECG中，由勾股定理得：（2+x）²=（6-x）²+4²，
x=3，
∴FC=BF+BC=3=6=9，
 在Rt△DFC中，DF=$\sqrt{{6}^{2}+{9}^{2}}$=3$\sqrt{13}$，
综上所述，DF的长为6$\sqrt{2}$或3$\sqrt{13}$；
故答案为：6$\sqrt{2}$或3$\sqrt{13}$．

点评 本题考查了正方形的性质、全等三角形的性质和判定，本题辅助线的作法是关键，利用辅助线构建全等三角形，并采用了分类讨论的思想，本题容易丢解，要注意利用数形结合的思想，解决问题．