
【题目】已知:在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图①,若AB=1,DG=2,求BH的长;
(2)如图②,连接AH、GH,求证:AH=GH且AH⊥GH.

【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)先根据勾股定理得出AB,DG,进而求出BF,即可得出结论;
(2)先判断△ABH≌△MFH,进而判断出△ADG≌△MFG.即可判断出△AGM为等腰直角三角形,即可得出结论;
(1)解:∵正方形中ABCD和正方形DEFG,
∴△ABD,△GDF为等腰直角三角形.
∵AB=1,DG=2,
∴由勾股定理得BD=![]() ,DF=
,DF=![]() .
.
∵B、D、F共线,
∴BF=![]() .
.
∵H是BF的中点,
∴BH=![]() BF=
BF=![]() ;
;
(2)如图1,延长AH交EF于点M,连接AG,GM,
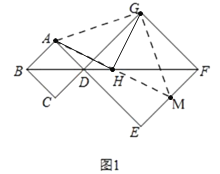
∵正方形中ABCD和正方形DEFG且B、D、F共线,
∴AB∥EF.
∴∠ABH=∠MFH.
又∵BH=FH,∠AHB=∠MHF,
∴△ABH≌△MFH.
∴AH=MH,AB=MF.
∵AB=AD,
∴AD=MF.
∵DG=FG,∠ADG=∠MFG=90°,
∴△ADG≌△MFG.
∴∠AGD=∠MGF,AG=MG.
又∵∠DGM+∠MGF=90°,
∴∠AGD+∠DGM=90°.
∴△AGM为等腰直角三角形.
∵AH=MH,
∴AH=GH,AH⊥GH.


科目:初中数学 来源: 题型:
【题目】如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
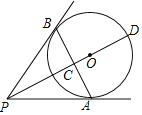
A. PA=PBB. ∠BPD=∠APDC. AB⊥PDD. AB平分PD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中, ![]() ,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为
,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为![]() cm,BD长为
cm,BD长为![]() cm(当D与A重合时,
cm(当D与A重合时, ![]() =4;当D与B重合时
=4;当D与B重合时![]() =0).
=0).
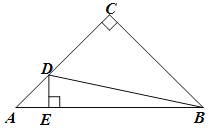
小云根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小云的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
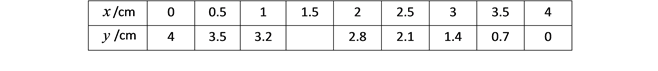
补全上面表格,要求结果保留一位小数.则![]() __________.
__________.
(2)在下面的网格中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当DB=AE时,AE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形是平行四边形,以AB为直径的![]() 经过点D, E是
经过点D, E是![]() 上一点,且
上一点,且![]() .
.
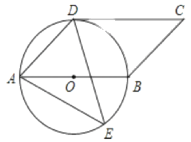
(1)判断CD与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2) 若BC=2 .求阴影部分的面积.(结果保留π 的形式).
查看答案和解析>>
科目:初中数学 来源: 题型:
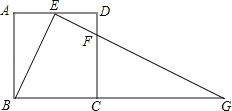
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,且E为AD的中点,FC=3DF,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为8,求△BEG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)求售价为多少元时每天获得利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某楼盘准备以每平方米15000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米12150元的均价开盘销售
![]() 求平均每次下调的百分率.
求平均每次下调的百分率.
![]() 某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
![]() 打
打![]() 折销售;
折销售;![]() 不打折,一次性送装修费每平方米250元.
不打折,一次性送装修费每平方米250元.
试问哪种方案更优惠?比另外一种方案优惠多少元?![]() 不考虑其他因素
不考虑其他因素![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用函数y=x2﹣4x+3的图象,直接回答:
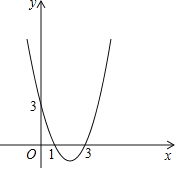
(1)方程x2﹣4x+3=0的解是 ;
(2)当x满足 时,函数值大于0.
(3)当0<x<5时,y的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com