
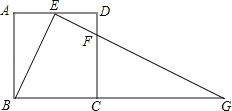
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,且E为AD的中点,FC=3DF,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为8,求△BEG的面积.
【答案】(1)详见解析;(2)80.
【解析】
(1)根据两边成比例夹角相等两三角形相似证明即可.
(2)证明△BAE∽△GEB,利用![]() =
=![]() ,求出EG即可解决问题.
,求出EG即可解决问题.
(1)证明:设正方形的边长为4a.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4a,∠A=∠D=90°,
∵AE=ED=2a,DF=a,CF=3a,
∴![]() =2,
=2,![]() =2,
=2,
∴![]() =
=![]() ,
,
∴△ABE∽△DEF.
(2)解:∵△ABE∽△DEF,
∴∠AEB=∠EFD,
∵∠EFD+∠DEF=90°,
∴∠AEB+∠DEF=90°,
∴∠BEF=90°,
∵AB=8,AE=4,∠A=90°,
∴BE=![]() =
=![]() =4
=4![]() ,
,
∵AE∥∥BG,
∴∠AEB=∠EBG,
∵∠A=∠BEG=90°,
∴△BAE∽△GEB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴EG=8![]()
∴EG=2![]() ,
,
∴S△BEG=![]() BEEG=
BEEG=![]() ×4
×4![]() ×8
×8![]() =80.
=80.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,经市场调査发现,该商品的周销售量y(件)是售价x(元/件)的一次函数.其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件) | 50 | 60 | 80 |
周销售量y(件) | 100 | 80 | 40 |
周销售利润w(元) | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价﹣进价)
(1)求y关于x的函数解析式_____;
(2)当售价是_____元/件时,周销售利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,1),B(1,-2),C(3,-1),P(m,n)是△ABC的边AB上一点.
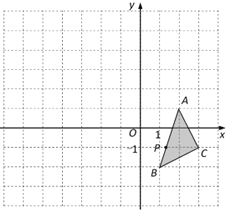
(1)画出△A1B1C1,使△A1B1C1与△ABC关于点O成中心对称,并写出点A、P的对应点A1、P1的坐标.
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出将△A1B1C1放大后的△A2B2C2,并分别写出点A1、P1的对应点A2、P2的坐标.
(3)求sin∠B2A2C2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图①,若AB=1,DG=2,求BH的长;
(2)如图②,连接AH、GH,求证:AH=GH且AH⊥GH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为8,则GE+FH的最大值为( )

A.8B.12C.16D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直线x=1.有以下结论:①abc>0;②7a+c<0;③a+b≤m(am+b)(m为任意实数)④若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;⑤若方程a(x+2)(4﹣x)=﹣1的两根为x1,x2,且x1<x2,则﹣2≤x1<x2<4.其中正确结论的个数有( )
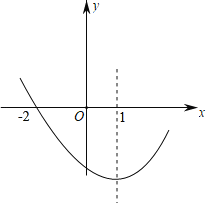
A.2个B.3个C.4个D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com