
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为8,则GE+FH的最大值为( )

A.8B.12C.16D.20
【答案】B
【解析】
首先连接OA、OB,根据圆周角定理,求出∠AOB=2∠ACB=60°,进而判断出△AOB为等边三角形;然后根据⊙O的半径为8,可得AB=OA=OB=8,再根据三角形的中位线定理,求出EF的长度;最后判断出当弦GH是圆的直径时,它的值最大,进而求出GE+FH的最大值是多少即可.
如图所示,连接OA、OB,

∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∵O的半径为8,
∴AB=OA=OB=8,
∵点E,F分别是AC、BC的中点,
∴EF=![]() AB=4,
AB=4,
∵GE+EF+FH=GH,EF为定值,
∴当GH最大时,GE+FH最大
∵当弦GH是圆的直径时,它的最大值为:8×2=16,
∴GE+FH的最大值为:164=12.
故选B.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() ,在
,在![]() 上取两点
上取两点![]() 在
在![]() 左边),以
左边),以![]() 为边作等边三角形
为边作等边三角形![]() ,使顶点
,使顶点![]() 在
在![]() 上.
上.
(1)求△PEF的边长;
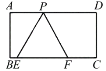
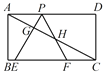
(2)若△PEF的边![]() 在线段
在线段![]() 上移动.
上移动.![]() 分别交
分别交![]() 于点
于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形是平行四边形,以AB为直径的![]() 经过点D, E是
经过点D, E是![]() 上一点,且
上一点,且![]() .
.
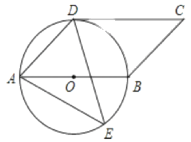
(1)判断CD与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2) 若BC=2 .求阴影部分的面积.(结果保留π 的形式).
查看答案和解析>>
科目:初中数学 来源: 题型:
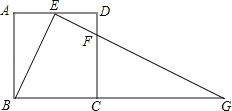
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,且E为AD的中点,FC=3DF,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为8,求△BEG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)求售价为多少元时每天获得利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生课余生活,计划开设以下课外活动项目:A—版画,B—机器人,C—航模,D—园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
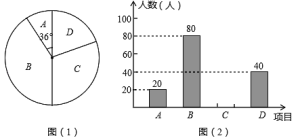
(1)这次被调查的学生共有 人;扇形统计图中,选“D—园艺种植”的学生人数所占圆心角的度数是 °
(2)请你将条形统计图补充完整;
(3)若该校学生总数为1000人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某楼盘准备以每平方米15000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米12150元的均价开盘销售
![]() 求平均每次下调的百分率.
求平均每次下调的百分率.
![]() 某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
![]() 打
打![]() 折销售;
折销售;![]() 不打折,一次性送装修费每平方米250元.
不打折,一次性送装修费每平方米250元.
试问哪种方案更优惠?比另外一种方案优惠多少元?![]() 不考虑其他因素
不考虑其他因素![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:PD=PF;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD为台球桌面,AD=240cm,AB=120cm,球目前在G点位置,AG=80cm,如果小丁瞄准BC边上的点F将球打过去,经过点F反弹后碰到CD边上的点H,再经过点H反弹后,球刚好弹到AD边的中点E处落袋.

(1)求证:△BGF∽△DHE;
(2)求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com