
����Ŀ��ͼ����һ����Ϊ![]() ����Ϊ
����Ϊ![]() �ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ��ͼ�ڵ���״ƴ��һ�������Σ�
�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ��ͼ�ڵ���״ƴ��һ�������Σ�




��1��ͼ���е���Ӱ���ֵ����Ϊ______��
��2���۲�ͼ������д����������ʽ![]() ��
��![]() ��
��![]() ֮��ĵ�����ϵ�ǣ�__________��
֮��ĵ�����ϵ�ǣ�__________��
��3��ʵ����������������ʽ������ͼ�ε��������ʾ����ͼ�ۣ�����ʾ��___________��
��4��������ͼ���ṩ�����ɿ鳤���κ�������ӲֽƬͼ�Σ���ƴ�����εķ����������ж�������ʽ������ʽ�ֽ⣺![]() ��Ҫ����ͼ�ܵĿ��л���ͼ�Σ�д���ֽ����ʽ��
��Ҫ����ͼ�ܵĿ��л���ͼ�Σ�д���ֽ����ʽ��
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��ͼ�μ�������
����4��ͼ�μ�������![]() ��
��
��������
��1���ô������ε������ȥ4��С�����ε�������������Ӱ���ֵ������
��2�����ô������ε��������4��С�����ε��������Ӱ�������֮�ɵó��𰸣�
��3�����ô��ε��������3��С�����κ�3��С�����ε����֮�ͼ��ɵó��𰸣�
��4���������ɸ�С�����κ�������ƴ��һ�����Σ�ʹ���ǵ����֮��Ϊ![]() ��Ȼ�����ƴ�ɵĴ��ε������ʽ���ɵõ���ʽ�ֽ�Ľ����
��Ȼ�����ƴ�ɵĴ��ε������ʽ���ɵõ���ʽ�ֽ�Ľ����
��1����Ӱ���ֵ����Ϊ
![]() ��
��
��2�����ݣ�1���Ľ����֪��![]() ��
��
��3�����ε�����ɱ�ʾΪ![]() ��
��
���ε����Ҳ�ɱ�ʾΪ![]() ��
��
��![]() ��
��
��4�������ɸ�С�����κ������ε����֮��Ϊ![]() ��
��
��ƴ�ɵĴ����л����1���߳�Ϊm�������Σ�3���߳�Ϊn�������κ�4����Ϊm����Ϊn�ij����Σ�
ƴ�ɵĴ�����ͼ��
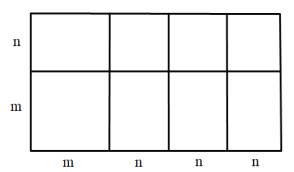
���ε�����ɱ�ʾΪ![]()
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ķ�������ʼװ�ޣ�����ʦͽ��������ˮ����֪ʦ�����������10�죬ͽ�ܵ��������15�졣
��1���������Ⱥ���2�죬ʣ�µ���ͽ�ܵ������������������Ԥ�ڵĹ���3����ɣ�������Ԥ�ڵĹ���������
��2����ʦ���Ĺ���ÿ��300Ԫ��ͽ�ܵĹ���ÿ��220Ԫ���������ӵ���ˮ����Ԥ�㲻����3180Ԫ����ʦ������Ҫ�����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶1������ίԱͳ����ȫ��ͬѧ60�������Ĵ����������Ƴ�����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
���� | 80��x��100 | 100��x��120 | 120��x��140 | 140��x��160 | 160��x��180 | 180��x��200 |
Ƶ�� | a | 4 | 12 | 16 | 8 | 3 |
���ͼ������������⣺
��1��a=�� ����
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��д��ȫ���������� �����������������120��x��140����Ƶ�ʣ���ȷ��0.01��
��4������������������140��ѧ���ɼ�Ϊ���㣬������ѧ������ռȫ���������İٷ�֮����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��OΪƽ��ֱ������ϵ��ԭ�㣬��A����Ϊ��4��0����ͬʱ����A��O�ֱ�����ƽ��2����λ��������ƽ��1����λ���õ���Ӧ��B��C��

��1�����ı���OABC�������
��2����y�����Ƿ����һ��M��ʹ��MOA��������ı���OABC�������ȣ�����������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
��3����ͼ2����P��OA���ϣ��ҡ�CBP=��CPB��Q��AO�ӳ�����һ���㣬��PCQ��ƽ����CD��BP���ӳ����ڵ�D���ڵ�Q�˶��Ĺ����У����D�͡�CQP��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�ᳫ��Լ��ˮ����ʵ������ˮ�����ݼƷѡ���ʽ���û���ˮ������������ˮ���IJ������ܻ����۸���������ˮ���IJ���ʵ�мӼ��շѣ�Ϊ���õؾ��ߣ�����ˮ��˾�����ȡ�����û������������ݣ������������²�����ͳ��ͼ��ÿ�����ݰ����Ҷ˵㵫��������˵㣩���������ͳ��ͼ����������⣺

��1���˴ε����ȡ�˶����û�����ˮ�����ݣ�
��2����ȫƵ������ֱ��ͼ��������ͳ��ͼ�С�25�֡�30�֡����ֵ�Բ�ĽǶ�����
��3���������ˮ��˾��������ˮ����Ϊÿ��25�֣���ô�õ�20���û���Լ�ж����û�����ˮȫ�����ܻ����۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ó���һ���IJ���ֲ�����Ƴ����Ϊ���εĿ�ܣ���ͼ�٢��е�һ�֣���������AB=x�ף����������ͼ���ش��������⣺�����еIJ���ֲ����ܳ���ָ��ͼ�����к��ߵij��Ⱥͣ����кᵵ�������ֱ���AD��ABƽ�У�
��1����ͼ���У��������ֲ����ܳ���Ϊ12�ף���xΪ����ʱ�����ο��ABCD�����Ϊ3ƽ���ף�
��2����ͼ���У��������ֲ����ܳ���Ϊ12�ף���xΪ����ʱ�����ο��ABCD�����S����������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊx=1����x���һ������Ϊ��x1��0�����ҩ�1��x1��0��������5�����ۣ���abc��0����9a��3b+c��0����2c��3b������a+c��2��b2����a+b��m��am+b����m��1��ʵ����������ȷ�Ľ����У�������
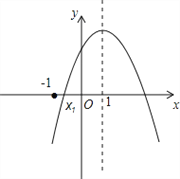
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��x���ཻ������A��1��0����B��3��0������y���ཻ�ڵ�C��0��3����
��1���������ߵĺ�����ϵʽ.
��2����y=ax2+bx+c����y=a��x��m��2+k����ʽ(��ֱ��д����).
��3������D��3.5��m����������y=ax2+bx+c�ϵ�һ�㣬�����m��ֵ���������ʱ��ABD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������13����
ij��˾����ũ��Ʒҵ����3��Ԫ/�ֵļ۸���ũ���չ�ũ��Ʒ�����ס������ַ�ʽ�������ۣ�����ʽ��װ��ֱ�����ۣ�����ʽ��ӹ���������������ʽũ��Ʒ�İ�װ�ɱ�Ϊ1��Ԫ/�֣������г����飬��ÿ��ƽ�����ۼ۸�y����λ����Ԫ����������m����λ������֮��ĺ�����ϵΪy = -m+14��2��m��8��������ʽũ��Ʒ��ӹ����������������ܷ���S����λ����Ԫ����������n����λ������֮��ĺ�����ϵ��S=3n+12��ƽ�����ۼ۸�Ϊ9��Ԫ/����
�ο���ʽ��������y��ax2+bx+c��a��0���Ķ�������������![]() ��
��![]() ��
��
��1���ù�˾�չ���20��ũ��Ʒ����������ʽ����ũ��Ʒx�֣�����ũ��Ʒ������ʽ���ۣ�������20��ũ��Ʒ����õ�ë����Ϊw��Ԫ��ë����=���������룭��Ӫ�ܳɱ�����
��ֱ��д��������ʽ����Ͱ�װx��ũ��Ʒ�����ʽ�Ϊ_________��Ԫ������ʽ����ͼӹ�����ũ��Ʒ�����ʽ�Ϊ_________��Ԫ��
�����w����x�ĺ�����ϵʽ��
����ũ��Ʒȫ�����۸ù�˾�������48��Ԫë������x��ֵ��
����ũ��Ʒȫ���۳����ù�˾����С�����Ƕ�����
��2���ù�˾���������ʽ�132��Ԫ���������������ʽ�ȫ�����ھ���ũ��Ʒ��
����������ʽ����ũ��Ʒx�֣����ܾ�����pΪ__________�����ú�x�Ĵ���ʽ��ʾ����
����xΪ��ֵʱ��ʹ��˾������ë����������ë������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com