
【题目】如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.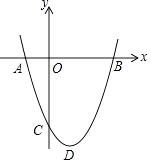
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BC,BE,求∠CBE的正切值;
(3)在(2)的条件下,点M是抛物线对称轴上且在CE上方的一点,是否存在点M使△DMB和△BCE相似?若存在,求点M坐标;若不存在,请说明理由.
【答案】
(1)
解:设抛物线的解析式为y=(x+3)(x+n),将点C的坐标代入得:3n=﹣3,解得n=﹣1.
∴抛物线的解析式为y=(x+3)(x﹣1)即y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4)
(2)
解:如图1所示:过点E作ED⊥BC,垂足为D.
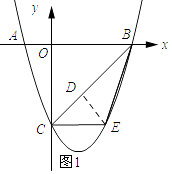
∵B(3,0),C(0,﹣3),
∴OC=OB=3.
∴∠OCB=∠OBC=45°,BC=3 ![]()
∵点E与点C关于抛物线的对称轴对称,
∴CE⊥OC,
∴∠DCE=45°.
∵ED⊥CD,
∴△DEB为等腰直角三角形.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴为x=1.
∴CE=2.
∴CD=ED= ![]() .
.
∴BD=BC﹣CD=2 ![]() .
.
∴tan∠CBE= ![]() =
= ![]()
(3)
解:如图2所示:
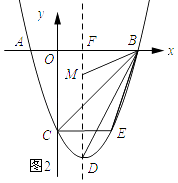
∵B(3,0),D(﹣1,﹣4),
∴A(﹣1,0),F(1,0).
∴FB=2,DF=4.
∴tan∠FDB= ![]() .
.
∴tan∠FDB=tan∠CBE.
∴∠FDB=∠CBE.
∴当 ![]() =
= ![]() 时,△BCE∽△DBM.
时,△BCE∽△DBM.
∴ ![]() =
= ![]() ,解得:MD=
,解得:MD= ![]() .
.
∴点M的纵坐标=﹣4+ ![]() =﹣
=﹣ ![]() .
.
∴M(1,﹣ ![]() ).
).
如图3所示:
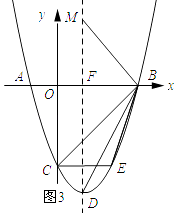
∵∠FDB=∠CBE,
∴当∠BMD=∠BCE=45°时,△DMB∽△BCE.
∴FM=FB=2.
∴M(1,2).
综上所述,当点M的坐标为(1,﹣ ![]() )或(1,2)时,△DMB和△BCE相似
)或(1,2)时,△DMB和△BCE相似
【解析】(1)设抛物线的解析式为y=(x+3)(x+n),将点C的坐标代入可求得n的值,则可得到抛物线的解析式,然后利用配方法可求得抛物线的顶点坐标;(2)过点E作ED⊥BC,垂足为D.由题意可得到△OBC和△CDE均为等腰直角三角形,然后求得CE、BC、DE的长,最后利用锐角三角函数的定义求解即可;(3)先证明tan∠FDB=tan∠CBE,从而得到∠FDB=∠CBE,当 ![]() =
= ![]() 或当∠BMD=∠BCE=45°时,△DMB和△BCE相似.
或当∠BMD=∠BCE=45°时,△DMB和△BCE相似.


科目:初中数学 来源: 题型:
【题目】如图填空:
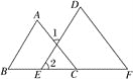
(1)∵∠1=∠A(已知),
∴_________(______________________);
(2)∵∠1=∠D(已知),
∴________(________________________);
(3)∵______=∠F(已知),
∴AC∥DF(______________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;
②当﹣1≤x≤3时,y<0;
③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )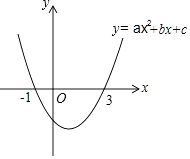
A.①②④
B.①②③
C.①④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
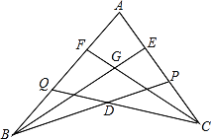
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE. 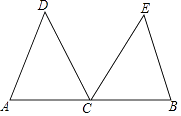
(1)求证:△ACD≌△BCE;
(2)若∠D=53°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是 .
(k<0)上运动,则k的值是 . 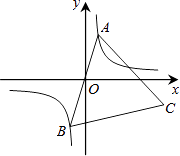
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com