
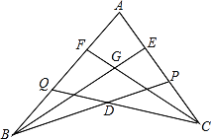
【题目】如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
科目:初中数学 来源: 题型:
【题目】为了进一步了解义务教育阶段学生的体质健康状况,某县从全县九年级学生中随机抽取了部分学生进行了体质抽测.体质抽测的结果分为四个等级:A级:优秀;B级:良好;C级:合格;D级:不合格.并根据抽测结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: 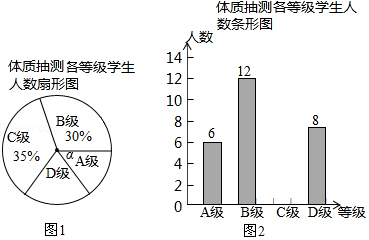
(1)本次抽测的学生人数是人;
(2)图(1)中∠α的度数是 , 并把图(2)条形统计图补充完整;
(3)该县九年级有学生4800名,如果全部参加这次体质测试,请估计不合格的人数为 .
(4)测试老师想从4位同学(分别记为E、F、G、H,其中H为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数的图像与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)一次函数的函数关系式;
(2)若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组条件中,不能判断△ABC≌△DEF的是( )
A. ∠A=∠D,AB=DE,∠B=∠E B. AB=DE,∠A=∠D,BC=EF
C. AB=DE,BC=EF,AC=DF D. ∠B=∠E=90°,AB=DE,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:
①图中全等三角形有三对;②△ABC的面积等于四边形CDOE面积的![]() 倍;③DE2+2CDCE=2OA2;④AD2+BE2=2OPOC.正确的有( )个.
倍;③DE2+2CDCE=2OA2;④AD2+BE2=2OPOC.正确的有( )个.
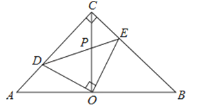
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
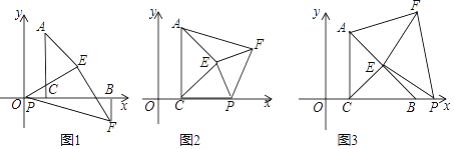
【题目】如图,在△ABC中,点B,C是x轴上的两个定点,∠ACB=90°,AC=BC,点A(l,3),点P是x轴上的一个动点,点E是AB的中点,在△PEF中,∠PEF=90°,PE=EF
(1)如图1,当点P与坐标原点重合时:①求证△PCE≌△FBE;②求点F的坐标;
(2)如图2,当点P在线段CB上时,求证S△CPE=S△AEF
(3)如图3,当点P在线段CB的延长线时,若S△AEF=4S△PBE则此刻点F的坐标为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.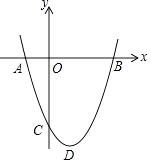
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BC,BE,求∠CBE的正切值;
(3)在(2)的条件下,点M是抛物线对称轴上且在CE上方的一点,是否存在点M使△DMB和△BCE相似?若存在,求点M坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师的数学课采用小组合作学习的方式,把班上40名学生分成若干个小组.如果要求每小组只能是5人或6人,那么分组方案有( )
A. 4种 B. 3种 C. 2种 D. 1种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com