
【题目】一次函数的图像与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)一次函数的函数关系式;
(2)若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;
【答案】(1)y=2x-2;(2)C(2,2)或C(-2,-6).
【解析】
(1)设直线AB的解析式为y=kx+b(k≠0),再把点A(1,0),点B(0,-2)代入得到k、b的方程组,解方程组得到k=2,b=-2,即可得直线AB的解析式为y=2x-2;(2)设点C的坐标为(x,y),由点B的坐标为(0 ,﹣2 )可得OB=2;由S△BOC=2,根据三角形的面积公式可得![]() ×2×〡x〡=2,解得x=±2,把x=±2代入直线AB的解析式求得y的值,即可求得点C的坐标.
×2×〡x〡=2,解得x=±2,把x=±2代入直线AB的解析式求得y的值,即可求得点C的坐标.
(1 )设直线AB 的解析式为y=kx+b ,
∵直线AB 过点A (1 ,0 )、点B (0 ,﹣2 ),
∴![]() ,
,
解得k=2,b=-2,
∴直线AB的解析式为y=2x﹣2.
(2)设点C的坐标为(x,y),
∵点B的坐标为(0 ,﹣2 ),
∴OB=2
∵S△BOC=2,
∴![]() ×2×〡x〡=2,解得x=±2,
×2×〡x〡=2,解得x=±2,
∴y=2×2-2=2或y=2×(-2)-2=-6.
∴点C的坐标是(2,2)或(-2,-6).


科目:初中数学 来源: 题型:
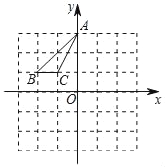
【题目】如图,在平面直角坐标系中,三角形ABC的顶点A、B、C的坐标分别为(0,3)、(﹣2,1)、(﹣1,1),如果将三角形ABC先向右平移2个单位长度,再向下平移2个单位长度,会得到三角形A′B′C′,点A'、B′、C′分别为点A、B、C移动后的对应点.
(1)请直接写出点A′、B'、C′的坐标;
(2)请在图中画出三角形A′B′C′,并直接写出三角形A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图填空:
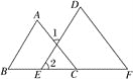
(1)∵∠1=∠A(已知),
∴_________(______________________);
(2)∵∠1=∠D(已知),
∴________(________________________);
(3)∵______=∠F(已知),
∴AC∥DF(______________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中.AB=AC.∠BAC=90![]() .E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
.E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
(l)图中是否存在两个三角形全等?如果存在请写出哪两个三角形全等,并且证明;如果不存在,请说明理由;
(2)若∠CBE=30![]() ,求∠ADC的度数.
,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:
计算代数式![]() (其中x≠0)的值后填入下表.并根据表格所反映出的
(其中x≠0)的值后填入下表.并根据表格所反映出的![]() (其中x≠0)的值与x之间的变化规律进行探究.
(其中x≠0)的值与x之间的变化规律进行探究.
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | …… |
下面是小东计算代数式![]() (其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
(其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | 2 | 1 |
|
|
|
| …… |
(1)上表是![]() (其中x≠0)与x的几组对应值.直接写出x=10时,求代数式
(其中x≠0)与x的几组对应值.直接写出x=10时,求代数式![]() 的值;
的值;
(2)随着x值的增大,代数式![]() 的值有何变化(回答“增大”或“减少”);
的值有何变化(回答“增大”或“减少”);
(3)当x值无限增大时,代数式![]() 的值无限趋近于一个数,这个数是多少.
的值无限趋近于一个数,这个数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第2 018个点的坐标为( )
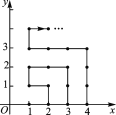
A. (45,9) B. (45,11) C. (45,7) D. (46,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;
②当﹣1≤x≤3时,y<0;
③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )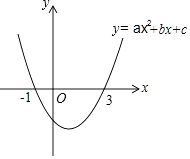
A.①②④
B.①②③
C.①④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
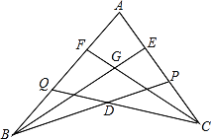
【题目】如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com