
分析 (1)首先求得抛物线的顶点坐标,根据坐标可以发现直线m是正比例函数,由此利用待定系数法求得答案即可;
(2)两个函数两立方程,设出交点坐标为(a,p),(b,q),利用根与系数的关系,以及两点之间的距离计算方法求得AB的长与n的函数关系式即可.
解答 解:(1)∵抛物线y=-$\frac{1}{2}$(x-3n)2+4n的顶点A为(3n,4n),
∴设直线m=kx,
代入解得k=$\frac{4}{3}$,
∴直线m的函数解析式y=$\frac{4}{3}$x;
(2)由题意得
-$\frac{1}{2}$(x-3n)2+4n=$\frac{4}{3}$x,
整理得:x2-(6n+6)x+9n2=0,
设函数的两个交点坐标为(a,p),(b,q),
则a+b=6n+6,ab=9n2,
(a-b)2=(a+b)2-4ab=72n+36;
(p-q)2=[$\frac{4}{3}$(a-b)]2=$\frac{16}{9}$[(a+b)2-4ab]=128n+64;
因此AB=$\sqrt{(a-b)^{2}+(p-q)^{2}}$=10$\sqrt{2n+1}$.
点评 此题考查二次函数的性质,待定系数法求函数解析式,两点之间的距离计算方法,根与系数的关系,综合性较强,注意数据的特点,选择适当的方法解决问题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 6 | C. | $\frac{7}{4}$$\sqrt{3}$ | D. | $\frac{9}{2}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
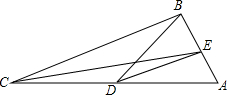 如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.
如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{5}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一个矩形广场的长为60m,宽为40m,广场内两条纵向小路的宽均为1.5m,如果设两条横向小路的宽都为x m,那么当x为多少时,小路内外边缘所围成的两个矩形相似?
如图,一个矩形广场的长为60m,宽为40m,广场内两条纵向小路的宽均为1.5m,如果设两条横向小路的宽都为x m,那么当x为多少时,小路内外边缘所围成的两个矩形相似?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x-1=$\frac{2}{3}-3x(x=\frac{1}{3})$ | B. | 1=$\frac{x}{2}-4$(x=-10) | ||
| C. | 4x+2=-x-3(x=1) | D. | 0.48x-6=0.02x(x=1.2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com