
【题目】抛物线y=ax2+bx﹣4与x轴交于A,B两点,(点B在点A的右侧)且A,B两点的坐标分别为(﹣2,0)、(8,0),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)在(2)的结论下,试问抛物线上是否存在点N(不同于点Q),使三角形BCN的面积等于三角形BCQ的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】
(1)
解:将A(﹣2,0),B(8,0)代入抛物线y=ax2+bx﹣4得:
![]() ,
,
解得: 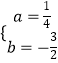 ,
,
∴抛物线的解析式:y= ![]() x2﹣
x2﹣ ![]() x﹣4
x﹣4
(2)
解:当x=0时,y=﹣4,
∴C(0,﹣4),
∴OC=4,
∵四边形DECB是菱形,
∴OD=OC=4,
∴D(0,4),
设BD的解析式为:y=kx+b,
把B(8,0)、D(0,4)代入得: ![]() ,
,
解得: 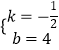 ,
,
∴BD的解析式为:y=﹣ ![]() x+4,
x+4,
∵l⊥x轴,
∴M(m,﹣ ![]() m+4)、Q(m,
m+4)、Q(m, ![]() m2﹣
m2﹣ ![]() m﹣4),
m﹣4),
如图1,∵MQ∥CD,
∴当MQ=DC时,四边形CQMD是平行四边形,
∴(﹣ ![]() m+4)﹣(
m+4)﹣( ![]() m2﹣
m2﹣ ![]() m﹣4)=4﹣(﹣4),
m﹣4)=4﹣(﹣4),
化简得:m2﹣4m=0,
解得m1=0(不合题意舍去),m2=4,
∴当m=4时,四边形CQMD是平行四边形

(3)
解:如图2,要使三角形BCN的面积等于三角形BCQ的面积,N点到BC的距离与Q到BC的距离相等;
设直线BC的解析式为:y=kx+b,
把B(8,0)、C(0,﹣4)代入得: ![]() ,
,
解得: 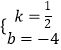 ,
,
∴直线BC的解析式为:y= ![]() x﹣4,
x﹣4,
由(2)知:当P(4,0)时,四边形DCQM为平行四边形,
∴BM∥QC,BM=QC,
得△MFB≌△QFC,
分别过M、Q作BC的平行线l1、l2,
所以过M或Q点的斜率为的 ![]() 直线与抛物线的交点即为所求,
直线与抛物线的交点即为所求,
当m=4时,y=﹣ ![]() m+4=﹣
m+4=﹣ ![]() ×4+4=2,
×4+4=2,
∴M(4,2),
当m=4时,y= ![]() m2﹣
m2﹣ ![]() m﹣4=
m﹣4= ![]() ×16﹣
×16﹣ ![]() ×4﹣4=﹣6,
×4﹣4=﹣6,
Q(4,﹣6),
①设直线l1的解析式为:y= ![]() x+b,
x+b,
∵直线l1过Q点时,
∴﹣6= ![]() ×4+b,b=﹣8,
×4+b,b=﹣8,
∴直线l1的解析式为:y= ![]() x﹣8,
x﹣8,
则 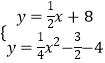 ,
,
![]() =
= ![]() x﹣8,
x﹣8,
解得x1=x2=4(与Q重合,舍去),
②∵直线l2过M点,
同理求得直线l2的解析式为:y= ![]() x,
x,
则 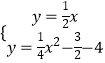 ,
,
![]() =
= ![]() x,
x,
x2﹣x﹣16=0,
解得x1=4+4 ![]() ,x2=4﹣4
,x2=4﹣4 ![]() ,
,
代入y= ![]() x,得
x,得 ![]() ,
, ![]() ,
,
则N1(4+4 ![]() ,2+2
,2+2 ![]() ),N2(4﹣4
),N2(4﹣4 ![]() ,2﹣2
,2﹣2 ![]() ),
),
故符合条件的N的坐标为N1(4+4 ![]() ,2+2
,2+2 ![]() ),N2(4﹣4
),N2(4﹣4 ![]() ,2﹣2
,2﹣2 ![]() ).
).
【解析】(1)直接将A、B两点的坐标代入抛物线的解析式中,列方程组可求a、b的值,写出解析式即可;(2)先求点C和D的坐标,求直线BD的解析式,根据横坐标m表示出点Q和M的纵坐标,由MQ∥CD,根据一组对边平行且相等的四边形是平行四边形,证明MQ=CD即可,因此列等式:(﹣ ![]() m+4)﹣(
m+4)﹣( ![]() m2﹣
m2﹣ ![]() m﹣4)=4﹣(﹣4),求m即可;(3)要使三角形BCN的面积等于三角形BCQ的面积,可先判断四边形CQBM是平行四边形,解得M点到BC的距离与Q到BC的距离相等,所以过M或Q点的与直线BC平行的直线与抛物线的交点即为所求,列方程组可得结论.
m﹣4)=4﹣(﹣4),求m即可;(3)要使三角形BCN的面积等于三角形BCQ的面积,可先判断四边形CQBM是平行四边形,解得M点到BC的距离与Q到BC的距离相等,所以过M或Q点的与直线BC平行的直线与抛物线的交点即为所求,列方程组可得结论.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面一列数,探求其规律:
![]() ,-
,-![]() ,
,![]() ,-
,-![]() ,
,![]() ,-
,-![]() ,…
,…
(1) 写出第7,8,9项的三个数;
(2) 第2 018个数是什么?
(3) 如果这一列数无限排列下去,与 ____ 、____ 两数越来越接近?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
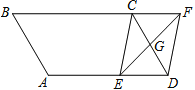
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个转盘,转盘被分成4个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率:
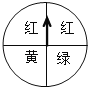
(1)指针指向绿色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空:
(a﹣b)(a+b)=
(a﹣b)(a2+ab+b2)=
(a﹣b)(a3+a2b+ab2+b3)=
(2)猜想:(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)= (其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:39﹣38+37﹣…+33﹣32+3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是用火柴棒拼出的一列图形.

仔细观察,找出规律,解答下列各题:
(1)第6个图中共有 根火柴;
(2)第n个图形中共有 根火柴(用含n的式子表示)
(3)第2017个图形中共有多少根火柴?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com