
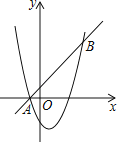
【题目】如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.
(1)求抛物线的解析式;
(2)点E是线段AB上一动点(点A,B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使∠PEF=90°?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)抛物线的解析式为y=x2-2x-3;(2)E(![]() ,
,![]() );点P的坐标为(1-
);点P的坐标为(1-![]() ,
,![]() )或(1+
)或(1+![]() ,
,![]() ).
).
【解析】
(1)先求得点A的坐标,然后将点A和点B的坐标代入抛物线的解析式可得到关于b、c的方程组,从而可求得b、c的值;
(2)设点E的坐标为(x,x+1),则点F的坐标为F(x,x2-2x-3),则可得到EF与x的函数关系式,利用配方法可求得EF的最大值以及点E的坐标;
(3)过点E作PE⊥EF,交抛物线与点P或点P′,则yp=![]() ,将y=
,将y=![]() 代入抛物线的解析式得:x2-2x-3=
代入抛物线的解析式得:x2-2x-3=![]() ,然后可求得点P的横坐标.
,然后可求得点P的横坐标.
(1)把y=0代入y=x+1得:x+1=0,解得:x=-1,
∴点A(-1,0).
将点A和点B的坐标代入抛物线的解析式得:
![]() ,
,
解得:b=-2,c=-3.
∴抛物线的解析式为y=x2-2x-3.
(2)如图1所示:
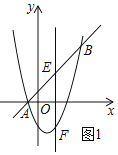
设点E的坐标为(x,x+1),则点F的坐标为F(x,x2-2x-3).
设EF=(x+1)-(x2-2x-3)=-x2+3x+4=-(x-![]() )2+
)2+![]() .
.
∴当x=![]() 时,EF有最大值.
时,EF有最大值.
将x=![]() 代入y=x+1得:y=
代入y=x+1得:y=![]() .
.
∴E(![]() ,
,![]() ).
).
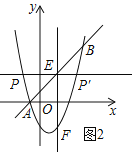
(3)如图2所示:过点E作PE⊥EF,交抛物线与点P或点P′,则yp=![]() .
.
将y=![]() 代入抛物线的解析式得:x2-2x-3=
代入抛物线的解析式得:x2-2x-3=![]() ,解得:x=1+
,解得:x=1+![]() ,x=1-
,x=1-![]() .
.
∴点P的坐标为(1-![]() ,
,![]() )或(1+
)或(1+![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A,对点A作如下变换:
第一步:作点A关于x轴的对称点A1;第二步:以O为位似中心,作线段OA1的位似图形OA2,且相似比![]() =q,则称A2是点A的对称位似点.
=q,则称A2是点A的对称位似点.
(1)若A(2,3),q=2,直接写出点A的对称位似点的坐标;
(2)已知直线l:y=kx-2,抛物线C:y=-![]() x2+mx-2(m>0).点N(
x2+mx-2(m>0).点N(![]() ,2k-2)在直线l上.
,2k-2)在直线l上.
①当k=![]() 时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
②若直线l与抛物线C交于点M(x1,y1)(x1≠0),且点M不是抛物线的顶点,则点M的对称位似点是否可能仍在抛物线C上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着2019年全国两会的隆重召开,中学生对时事新闻的关注空前高涨,某校为了解中学生对时事新闻的关注情况,组织全校九年级学生开展“时事新闻大比拼”比赛,随机抽取九年级的25名学生的成绩(满分为100分)整理统计如下:收集数据 25名学生的成绩(满分为100分)统计如下(单位:分)
90 ,74 ,88 ,65 ,98 ,75 , 81 ,44 ,85 ,70 ,55 , 80 , 95 ,88 ,72 ,87 , 60 ,56 ,76 ,66 ,78 ,72 ,82 ,63 ,100
整理数据:按如下分组整理样本数据并补全表格:
成绩 | 90≤ | 75≤ | 60≤ |
|
人数 | 10 | 8 |
分析数据 补充完成下面的统计分析表:
平均数 | 中位数 | 方差 |
76 | 190. 88 |
得出结论:
(1)若全校九年级有1000名学生,请估计全校九年级有多少学生成绩达到90分及以上;
(2)若八年级的平均数为76分,中位数为80分,方差为102. 5,请你分别从平均数、中位数和方差三个方面做出评价,你认为哪个年级的成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
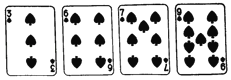
【题目】当当和叮叮玩纸牌游戏:如图是同一副扑克牌中的4张黑桃牌的正面,将这4张牌正面朝下洗匀后放在桌上,当当先从中抽出一张,叮叮从剩余的3张牌中也抽出一张,比较两人抽出的牌面上的数字,数字大者获胜.
(1)求当当抽出的牌面上的数字为6的概率;
(2)该游戏是否公平?请用画树状图或列表的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
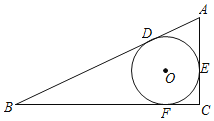
【题目】如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.
(1)求BF的长;
(2)求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面完全相同的A,B,C,D四张卡片,其正面分别画有四种不同是图形:正三角形、正方形、平行四边形、圆,现将四张卡片背面向上后洗均匀.
(1)从中任意摸出一张卡片,求摸到的卡片上画有轴对称图形的概率;
(2)从中任意摸出两张卡片,求两次摸到的卡片上所画图形既是中心对称图形又是轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,过AB边上点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使ED=CG,连接AE,CD.

(1)求证:AE=DC;
(2)过E作EF∥DC,交BC于点F,求证:∠AEF=∠ACB.
查看答案和解析>>
科目:初中数学 来源: 题型:
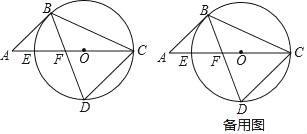
【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com