
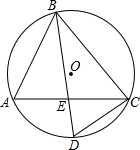
 如图,△ABC内接于⊙O,D为$\widehat{AC}$的中点,BD交AC于点E.
如图,△ABC内接于⊙O,D为$\widehat{AC}$的中点,BD交AC于点E.分析 (1)根据相似三角形的判定方法得△CDE∽△BDC,根据相似三角形的性质得到$\frac{DE}{DC}=\frac{DC}{BD}$,即可得到结论;
(2)连接OD交AC于F,OC,根据垂径定理得到OD⊥AC,OF=1,根据勾股定理列方程即可得到结论.
解答 解:(1)∵D为$\widehat{AC}$的中点,
∴∠ABD=∠CBD,
∵∠ABD=∠ACD,
∴∠DBC=∠ACD,
∵∠D为公共角,
∴△CDE∽△BDC,
∴$\frac{DE}{DC}=\frac{DC}{BD}$,
∴CD是DE和BD的比例中项;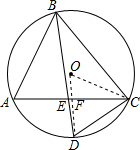 (2)连接OD交AC于F,OC,
(2)连接OD交AC于F,OC,
∵D为$\widehat{AC}$的中点,
∴OD⊥AC,OF=1,
∴CF2=CD2-DF2=OC2-OF2,
∴(2$\sqrt{3}$)2-(OC-1)2=OC2-1,
∴OC=3,
∴⊙O的半径是3.
点评 本题考查了相似三角形的判定和性质,圆周角定理,垂径定理,勾股定理,正确的作出辅助线构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
| 路程/km | 每百千米耗油量/L | 油价 (元/L) | 过桥费/元 | 票价 元/人 | |
| 甲 | 60 | 14 | 3 | 20 | 16 |
| 乙 | 64 | 10 | 3 | 5 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(a2-16) | B. | a(a+16)(a-1) | C. | a(a+16)(a-16) | D. | a(a+4)(a-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com