
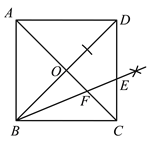
【题目】正方形ABCD的对角线AC,BD交于点O,作∠CBD的角平分线BE,分别交CD,OC于点E,F.
(1)依据题意,补全图形(用尺规作图,保留作图痕迹);
(2)求证:CE=CF;
(3)求证:DE=2OF.

【答案】(1)作图见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)按照“用直尺和圆规作角的平分线的一般步骤作图”即可;
(2)由已知条件易得∠BOF=∠BCE=90°,∠CFE=∠BFO,∠BFO+∠OBF=90°,∠CEF+∠CBE=90°,再结合由BE平分∠CBD所得的∠DBE=∠CBE即可得到∠CFE=∠CEF,由此可得CE=CF;
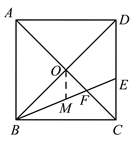
(3)如图1,取BE的中点M,连接OM.结合已知条件易得OM是△BDE的中位线,从而可得DE=2OM,OM∥DE,结合(2)中所得CE=CF可得∠AMF=∠CEF=∠CFE=∠OFM,由此可得OF=OM,则可得得到DE=2OF.
(1)如下图,射线BE为所求角平分线:
(2)∵BE平分∠CBD,
∴∠CBE=∠DBE.
∵正方形ABCD的对角线AC,BD交于点O,
∴∠BOC=∠BCD=90°.
∵∠CBE+∠CEB=90°,∠DBE+∠BFO=90°,
∴∠CEB=∠BFO.
∵∠EFC=∠BFO,
∴∠EFC=∠CEB.
∴CF=CE.
(3)取BE的中点M,连接OM.
∵O为AC的中点,
∴OM∥DE, DE=2OM.
∴∠OMF=∠CEF.
∵∠OFM=∠EFC=∠CEF,
∴∠OMF=∠OFM.
∴OF=OM.
∴DE=2OF.


科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD= 2,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() .
.
(1)试按要求画图:
①连接![]() ,作射线
,作射线![]() ;
;
②画点![]() ,使
,使![]() 的值最小;
的值最小;
③画点![]() ,使点
,使点![]() 既在直线
既在直线![]() 上又在直线
上又在直线![]() 上.
上.
(2)填空:若点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,
上,![]() ,
,![]() ,则
,则![]() 的长为 .
的长为 .
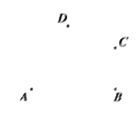
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在直线
在直线![]() 上,在直线
上,在直线![]() 的同侧,作射线
的同侧,作射线![]() 平分
平分![]() .
.
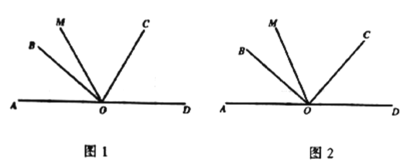
(1)如图1,若![]() ,
,![]() ,直接写出
,直接写出![]() 的度数为 ,
的度数为 ,![]() 的度数为 ;
的度数为 ;
(2)如图2,若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() 和
和![]() 互为余角且
互为余角且![]() ,
,![]() 平分
平分![]() ,试画出图形探究
,试画出图形探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴表示的是5个城市的国际标准时间(单位:时),如果北京的时间是2020年1月9日上午9时,下列说法正确的是( )

A.伦敦的时间是2020年1月9日凌晨1时
B.纽约的时间是2020年1月9日晚上20时
C.多伦多的时间是2020年1月8日晚上19时
D.汉城的时间是2020年1月9日上午8时
查看答案和解析>>
科目:初中数学 来源: 题型:
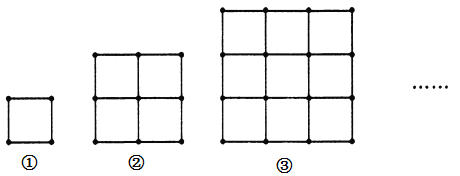
【题目】如图,用火柴棍摆出一列正方形图案,其中图①有4根火柴棍,图②有12根火柴棍,图③有24根火柴棍,![]() ,则图⑩中火柴棍的根数是( )
,则图⑩中火柴棍的根数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com