
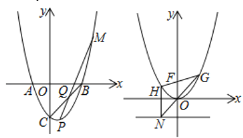
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,﹣2),顶点为P
(1)求抛物线的解析式;
(2)如图,若直线PM与BC交于Q,且sin∠CQP=![]() ,求点M的坐标;
,求点M的坐标;
(3)将抛物线平移至顶点为坐标原点,过F(0,![]() )的直线交抛物线于G、H,GO交直线y=﹣
)的直线交抛物线于G、H,GO交直线y=﹣![]() 于点N,求证:HN∥y轴.
于点N,求证:HN∥y轴.
【答案】(1)y=x2﹣x﹣2;(2)M(![]() ,
,![]() );(3)见解析
);(3)见解析
【解析】
(1)函数的表达式为:y=a(x+1)(x﹣2)=a(x2﹣x﹣2),即可求解;
(2)过点C作PM的平行线交x轴于点H,过点H作HG⊥BC于点G,求出点H(![]() ,0),确定直线PQ的表达式,即可求解.
,0),确定直线PQ的表达式,即可求解.
(3)直线HG的表达式为:y=x2x,则点N的坐标为(﹣![]() ,﹣
,﹣![]() ),由一元二次方程根与系数的关系得:x1x2=﹣
),由一元二次方程根与系数的关系得:x1x2=﹣![]() ,则x1=﹣
,则x1=﹣![]() ,即可求解.
,即可求解.
(1)函数的表达式为:y=a(x+1)(x﹣2)=a(x2﹣x﹣2),
故﹣2a=﹣2,解得:a=1,
故函数的表达式为:y=x2﹣x﹣2;
(2)过点C作PM的平行线交x轴于点H,过点H作HG⊥BC于点G,
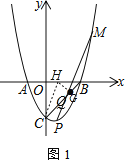
则∠HCB=∠CQP,
∵OB=OC=2,
∴∠OBC=45°,
设:OH=m,则BH=2﹣m,HG=BHsin∠OBC=![]() (2﹣m),HC=
(2﹣m),HC=![]() ,
,
sin∠HCB=![]() =sin∠CQP=
=sin∠CQP=![]() ,即:
,即: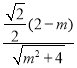 =
=![]() ,
,
解得:m=![]() (不合题意的值已舍去),则点H(
(不合题意的值已舍去),则点H(![]() ,0),
,0),
则直线CH表达式中的k值为:3,
设直线PQ的表达式为:y=3x+n,
将点(![]() ,﹣
,﹣![]() )的坐标代入上式并解得:
)的坐标代入上式并解得:
直线PM的表达式为:y=3x﹣![]() …②,
…②,
联立①②并解得:x=![]() 或
或![]() (舍去
(舍去![]() ),
),
故点M(![]() ,
,![]() );
);
(3)新函数的表达式为:y=x2…③,
设点H、G的坐标分别为(x1,x12)、(x2,x22),
则直线HG的表达式为:y=x2x,
则点N的坐标为(﹣![]() ,﹣
,﹣![]() );
);
设直线HG的表达式为:y=kx+![]() …④,
…④,
联立③④并整理得:x2﹣kx﹣![]() =0,
=0,
则x1x2=﹣![]() ,x1=﹣
,x1=﹣![]()
则点H的横坐标为:﹣![]() ,
,
点H、N的横坐标均为:﹣![]() ,
,
故HN∥y轴.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
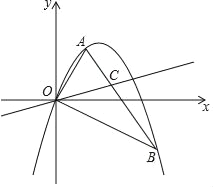
【题目】如图,抛物线y=ax2+bx经过△OAB的三个顶点,其中点A(1,![]() ),点B(3,﹣
),点B(3,﹣![]() ),O为坐标原点.
),O为坐标原点.
(1)求这条抛物线所对应的函数表达式;
(2)若P(4,m),Q(t,n)为该抛物线上的两点,且n<m,求t的取值范围;
(3)若C为线段AB上的一个动点,当点A,点B到直线OC的距离之和最大时,求∠BOC的大小及点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
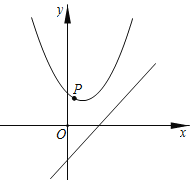
【题目】已知,抛物线y=![]() x2﹣x+2与直线y=x﹣2的图象如图,点P是抛物线上的一个动点,则点P到直线y=x﹣2的最短距离为( )
x2﹣x+2与直线y=x﹣2的图象如图,点P是抛物线上的一个动点,则点P到直线y=x﹣2的最短距离为( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题:
(1)写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称;
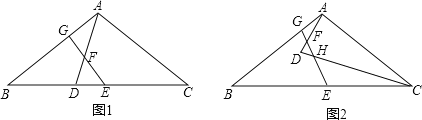
(2)如图1,在△ABC中,AB=AC,点D在BC上,且CD=CA,点E、F分别为BC、AD的中点,连接EF并延长交AB于点G.求证:四边形AGEC是等邻角四边形;
(3)如图2,若点D在△ABC的内部,(2)中的其他条件不变,EF与CD交于点H,图中是否存在等邻角四边形,若存在,指出是哪个四边形,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某学校有一边长为20米的正方形![]() 区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形
区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形![]() ,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
区域 | 甲 | 乙 |
价格(百元米2) | 6 | 5 |
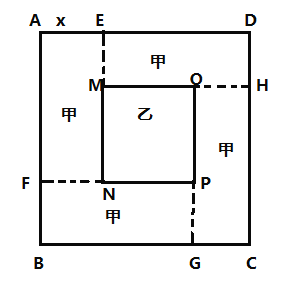
设矩形的较短边![]() 的长为
的长为![]() 米,正方形
米,正方形![]() 区域建设总费用为
区域建设总费用为![]() 百元.
百元.
(1)![]() 的长为 米(用含
的长为 米(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长要求不低于8米且不超过12米时,预备建设资金220000元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一元二次方程x2+2x﹣3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
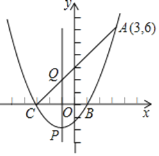
(1)求此二次函数的解析式;
(2)写出不等式ax2+bx+c≥0的解集;
(3)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标;
(4)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
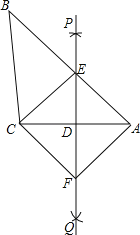
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若ED=6,AE=10,则菱形AECF的面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com