
分析 由a的值即使得不等式组$\left\{\begin{array}{l}\frac{x-a}{3}≥1\\ 2x-3≤-1\end{array}\right.$无解,可求得a=-1,0,1,2;又由在函数y=$\frac{1}{{x}^{2}-2x}$的自变量取值范围内,a=-3,-2,-1,1,继而求得答案.
解答 解:$\left\{\begin{array}{l}{\frac{x-a}{3}≥1①}\\{2x-3≤-1②}\end{array}\right.$,
由①得:x≥3+a,
由②得:x≤1,
∵不等式组$\left\{\begin{array}{l}\frac{x-a}{3}≥1\\ 2x-3≤-1\end{array}\right.$无解,
∴3+a>1,
解得:a>-2,
∴a=-1,0,1,2;
∵x2-2x≠0,
∴x≠2且x≠0,
∴a=-3,-2,-1,1;
∴a=-1,1;
∴a的值即使得不等式组$\left\{\begin{array}{l}\frac{x-a}{3}≥1\\ 2x-3≤-1\end{array}\right.$无解,又在函数y=$\frac{1}{{x}^{2}-2x}$的自变量取值范围内的概率为:$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了概率公式的应用以及不等式组的解集.用到的知识点为:概率=所求情况数与总情况数之比.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:填空题
 2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.
2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.| 组别 | 焦点话题 | 频数(人数) |
| A | 延迟退休 | 120 |
| B | 汽车尾号限行 | 80 |
| C | 就业养老 | m |
| D | 教育医疗 | n |
| E | 生态环保 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
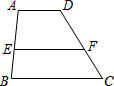 四边形ABCD中,E、F分别为AB、CD上的点,且AD∥EF∥BC,AE:EB=3:2,AD=2cm,BC=4cm,则EF=$\frac{16}{5}$cm.
四边形ABCD中,E、F分别为AB、CD上的点,且AD∥EF∥BC,AE:EB=3:2,AD=2cm,BC=4cm,则EF=$\frac{16}{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
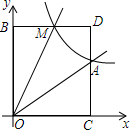 已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).
已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com