
【题目】已知坐标平面内的三个点![]() 、
、![]() 、
、![]() .
.
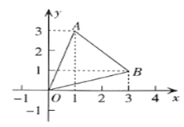
(1)比较![]() 点到
点到![]() 轴的距离与
轴的距离与![]() 点到
点到![]() 轴距离的大小;
轴距离的大小;
(2)平移![]() 至
至![]() ,当点
,当点![]() 和点
和点![]() 重合时,求点
重合时,求点![]() 的坐标;
的坐标;
(3)平移![]() 至
至![]() ,需要至少向下平移超过 单位,并且至少向左平移 个单位,才能使
,需要至少向下平移超过 单位,并且至少向左平移 个单位,才能使![]() 位于第三象限.
位于第三象限.
【答案】(1)![]() 点到
点到![]() 轴的距离等于
轴的距离等于![]() 点到
点到![]() 轴距离; (2)
轴距离; (2)![]() ;(3)3 ,3
;(3)3 ,3
【解析】
(1)根据横坐标为点到y轴的距离;纵坐标为点到x轴的距离即可比较大小;
(2)由点A1和点B重合时,需将△ABC向右移2个单位,向下移2个单位,据此求解可得;
(3)根据点A的纵坐标得出向下平移的距离,由点B的横坐标得出向左平移的距离.
解:(1)∵![]() ,
,
∴![]() 点到
点到![]() 轴的距离为3
轴的距离为3
∵![]() ,
,![]() 点到
点到![]() 轴距离为3
轴距离为3
∴![]() 点到
点到![]() 轴的距离等于
轴的距离等于![]() 点到
点到![]() 轴距离
轴距离
(2)点![]() 和点
和点![]() 重合时,需将
重合时,需将![]() 向右移2个单位,向下移2个单位,
向右移2个单位,向下移2个单位,
∴点![]() 的对应点
的对应点![]() 的坐标是
的坐标是![]()
(3)平移△ABO至△A2B2O2,需要至少向下平移超过3单位,并且至少向左平移3个单位,才能△A2B2O2使位于第三象限.
故答案为:3,3.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:某列车平均提速80km/h,用相同的时间,该列车提速前行驶300km,提速后比提速前多行驶200km,求该列车提速前的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在相距90千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,逆流航行比顺流航行多用4小时.
(1)求该轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少干米?
查看答案和解析>>
科目:初中数学 来源: 题型:
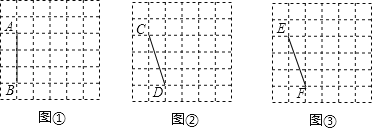
【题目】图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点![]() 均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中以线段![]() 为边画一个
为边画一个![]() ,使其面积为6.
,使其面积为6.
(2)在图②中以线段![]() 为边画一个
为边画一个![]() ,使其面积为6.
,使其面积为6.
(3)在图③中以线段![]() 为边画一个四边形
为边画一个四边形![]() ,使其面积为9,且
,使其面积为9,且![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
A工地 | B工地 | |
甲工程队 | 800元 | 750元 |
乙工程队 | 600元 | 570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
(1)求y与x之间的函数关系式;
(2)请判断y是否能等于62000,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市开展早市促销活动,为早到的顾客准备一份简易早餐,餐品为四样A:菜包、B:面包、C:鸡蛋、D:油条.超市约定:随机发放,早餐一人一份,一份两样,一样一个.
(1)按约定,“某顾客在该天早餐得到两个鸡蛋”是 事件(填“随机”、“必然”或“不可能”);
(2)请用列表或画树状图的方法,求出某顾客该天早餐刚好得到菜包和油条的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
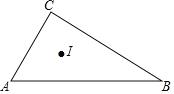
【题目】已知∠ACB=90°,∠CAB=a,且sina=![]() ,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步丰富校园活动,学校准备购买一批足球和篮球,已知购买7个足球和5个篮球的费用相同;购买40个足球和20个篮球共需3400元.
(1)求每个足球和篮球各多少元?
(2)如果学校计划购买足球和篮球共80个,总费用不超过4800元,那么最多能买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com