
【题目】如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.则HE的长为( )
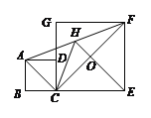
A. 2B. ![]() C. 2
C. 2![]() D.
D. ![]() 或2
或2![]()
科目:初中数学 来源: 题型:
【题目】操作:在△ABC中,AC=BC=4,∠C=90°,将一块直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。如图①、②、③是旋转三角板得到的图形中的3种情况。
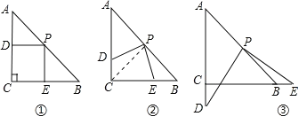
探究:
(1)如图①,PD⊥AC于D,PE⊥BC于E,则重叠部分四边形DCEP的面积为___,周长___.
(2)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②加以证明;
(3)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A1,与y轴交于点A2,过点A1作x轴的垂线交直线
与x轴交于点A1,与y轴交于点A2,过点A1作x轴的垂线交直线![]() 于点B1,过点A1作A1B1的垂线交y轴于点B2,此时点B2与原点O重合,连接A2B1交x轴于点C1,得到第1个
于点B1,过点A1作A1B1的垂线交y轴于点B2,此时点B2与原点O重合,连接A2B1交x轴于点C1,得到第1个![]() ;过点A2作y轴的垂线交l2于点B3,过点B3作y轴的平行线交l1于点A3,连接A3B2与A2B3交于点C2,得到第2个
;过点A2作y轴的垂线交l2于点B3,过点B3作y轴的平行线交l1于点A3,连接A3B2与A2B3交于点C2,得到第2个![]() ……按照此规律进行下去,则第2019个
……按照此规律进行下去,则第2019个![]() 的面积是________.
的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是( )

A. AB=CD,AB⊥CDB. AB=CD,AD=BC
C. AB=CD,AC⊥BDD. AB=CD,AD∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图1,在等边△ABC中,AB=4,点D、E分别为边BC、AB上的点,连结AD、DE,若∠ADE=60°,BD=3,求BE的长.

(拓展)如图2,在△ABD中,AB=4,点E为边AB上的点,连结DE,若∠ADE=∠ABD=45°,若DB=3![]() ,
,![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别在正方形ABCD的边CD,BC上,且![]() ,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转
,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转![]() 得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.
得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.
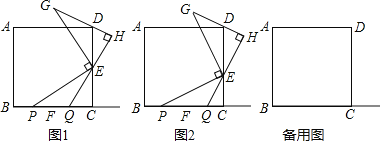
(1)如图1,若点E是CD的中点,点P在线段BF上,线段BP,QC,EC的数量关系为________.
(2)如图2,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形ABCD的边长为6,![]() ,
,![]() ,请直接写出线段BP的长.
,请直接写出线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点的直线与反比例函数y=![]() (x>0)、反比例函数y=
(x>0)、反比例函数y=![]() (x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y=
(x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y=![]() (x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为______.
(x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为______.
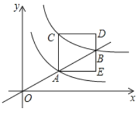
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某商品进价每件 40 元,现售价每件 60 元,每星期可卖出 300 件,经市场调查反映,每次涨价 1 元,每星期可少卖 10 件
(1)要想获利 6090 元的利润,该商品应定价多少元?
(2)能否获利 7000 元,试说明理由?
(3)该商品应定价多少元时,获利最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com