
【题目】(探究)如图1,在等边△ABC中,AB=4,点D、E分别为边BC、AB上的点,连结AD、DE,若∠ADE=60°,BD=3,求BE的长.

(拓展)如图2,在△ABD中,AB=4,点E为边AB上的点,连结DE,若∠ADE=∠ABD=45°,若DB=3![]() ,
,![]() = .
= .
【答案】【探究】BE=![]() ;【拓展】
;【拓展】![]()
【解析】
探究:过点A作AF⊥BC于F,由等边三角形的性质得出BF=CF=![]() BC=2,由勾股定理求出AF=
BC=2,由勾股定理求出AF=![]() ,则DF=BD-BF=1,由勾股定理求出AD=
,则DF=BD-BF=1,由勾股定理求出AD=![]() ,证得△ABD∽△ADE,得出
,证得△ABD∽△ADE,得出![]() ,解得AE=
,解得AE=![]() ,即可得出结果;
,即可得出结果;
拓展:过点A作AF⊥BC于F,易证△ABF是等腰直角三角形,则AF=BF=![]() AB=2
AB=2![]() ,DF=DB-BF=
,DF=DB-BF=![]() ,由勾股定理求出AD=
,由勾股定理求出AD=![]() ,证得△ADE∽△ABD,得出
,证得△ADE∽△ABD,得出![]() ,求出AE=
,求出AE=![]() ,BD=AB-AE=
,BD=AB-AE=![]() ,则
,则![]() 即可得出结果.
即可得出结果.
探究:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC=4,
过点A作AF⊥BC于F,如图①所示:
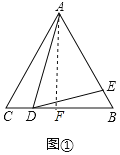
则BF=CF=![]() BC=2,AF=
BC=2,AF=![]() ,
,
∴DF=BD-BF=3-2=1,
∴AD=![]() ,
,
根据三角形的内角和定理得,∠ADB+∠BAD=120°,
∵∠ADE=60°,
∴∠BAD+∠AED=120°,
∴∠ADB=∠AED,
∵∠B=∠ADE=60°,
∴△ABD∽△ADE,
∴![]() ,
,
即:![]() ,
,
解得:AE=![]() ,
,
∴BE=AB-AE=4-![]() =
=![]() ;
;
拓展:过点A作AF⊥BC于F,如图②所示:
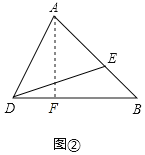
∵∠ABD=45°,
∴△ABF是等腰直角三角形,
∴AF=BF=![]() AB=2
AB=2![]() ,
,
∴DF=DB-BF=3![]() -2
-2![]() =
=![]() ,
,
∴AD=![]() ,
,
∵∠ADE=∠ABD=45°,∠A=∠A,
∴△ADE∽△ABD,
∴![]() ,
,
∴AE=![]() ,
,
∴BD=AB-AE=4-![]() =
=![]() ,
,
∴ .
.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3过A(﹣3,0),B(1,0)两点,交y轴于点C.
(1)求该抛物线的表达式.
(2)设P是该抛物线上的动点,当△PAB的面积等于△ABC的面积时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1).
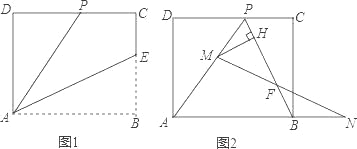
(1)求AB的长;
(2)擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).
①若M是PA的中点,求MH的长;
②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且
,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且![]() ,连接MP交AC于点H.将射线MP绕点M逆时针旋转
,连接MP交AC于点H.将射线MP绕点M逆时针旋转![]() 交线段CA的延长线于点D.
交线段CA的延长线于点D.
(1)找出与![]() 相等的角,并说明理由.
相等的角,并说明理由.
(2)如图2,![]() ,求
,求![]() 的值.
的值.
(3)在(2)的条件下,若![]() ,求线段AB的长.
,求线段AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.则HE的长为( )
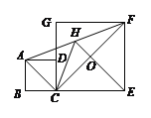
A. 2B. ![]() C. 2
C. 2![]() D.
D. ![]() 或2
或2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“绿色生活,美丽家园”号召,某社区计划种植甲、乙两种花卉来美化小区环境.若种植甲种花卉![]() ,乙种花卉
,乙种花卉![]() ,共需430元;种植甲种花卉
,共需430元;种植甲种花卉![]() ,乙种花卉
,乙种花卉![]() ,共需260元.
,共需260元.
(1)求:该社区种植甲种花卉![]() 和种植乙种花卉
和种植乙种花卉![]() 各需多少元?
各需多少元?
(2)该社区准备种植两种花卉共![]() 且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
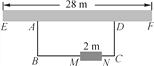
【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形。

(1)求证AE=CG,并说明理由。
(2)连接AG,若AB=17,DG=13,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com