练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

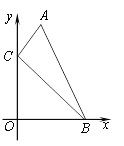
    【题目】如图，在直角坐标系中，点A，B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A，B，C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是____________．

    【答案】(0，3)

    【解析】

    由题意根据轴对称做最短路线得出AE=B′E，进而得出B′O=C′O，即可得出△ABC的周长最小时C点坐标．

    解：作B点关于y轴对称点B′点，连接AB′，交y轴于点C′，

    此时△ABC的周长最小，

    ∵点A、B的坐标分别为（1，4）和（3，0），

    ∴B′点坐标为：（-3，0），AE=4，

    则B′E=4，即B′E=AE，

    ∵C′O∥AE，

    ∴B′O=C′O=3，

    ∴点C′的坐标是（0，3），此时△ABC的周长最小．

    故答案为：（0，3）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在新冠疫情防控期间，某医疗器械商业集团新进了40台A型电子体温测量仪，60台B型电子体温测量仪，计划调配给下属的甲、乙两个连锁店销售，其中70台给甲连锁店，30台给乙连锁店．两个连锁店销售这两种测量仪每台的利润(元)如下表：

    A型

    B型

    甲连锁店

    200

    170

    乙连锁店

    160

    150

    设集团调配给甲连锁店台A型测量仪，集团卖出这100台测量仪的总利润为(元)．

    （1）求关于的函数关系式，并求出的取值范围：

    （2）为了促销，集团决定仅对甲连锁店的A型测量仪每台让利元销售，其他的销售利润不变，并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润，问该集团应该如何设计调配方案，使总利润达到最大?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

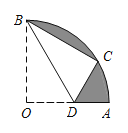
    【题目】如图，在扇形AOB中，∠AOB=90°，半径OA=4．将扇形AOB沿过点B的直线折叠，点O恰好落在弧AB上点C处，折痕交OA于点D，则图中阴影部分的面积为_______ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

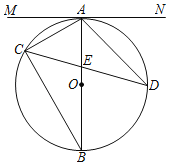
    【题目】如图，△ABC内接于⊙O，AB是⊙O的直径，弦CD与AB交于点E，连接AD，过点A作直线MN，使∠MAC＝∠ADC．

    （1）求证：直线MN是⊙O的切线．

    （2）若sin∠ADC＝，AB＝8，AE＝3，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）作图：作∠MON的平分线OE，在OE上任取一点A，过A作AB∥OM，AC∥ON，连接BC交OA于D．（只保留作图痕迹）

    （2）BC与OA的位置关系是什么？请加以证明．

    （3）若OA=8，AC=5，则BD是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线过点A(－1，0)，B(4，0)，与y轴相交于点C．

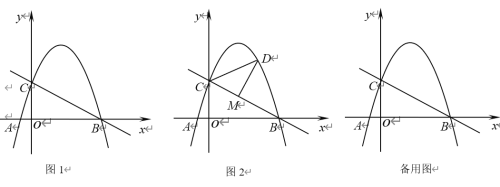
    （1）求抛物线的解析式；

    （2）在x轴正半轴上存在点E，使得△BCE是等腰三角形，请求出点E的坐标；

    （3）如图2，点D是直线BC上方抛物线上的一个动点．过点D作DM⊥BC于点M，是否存在点D，使得△CDM中的某个角恰好等于∠ABC的2倍？若存在，请求出点D的横坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，二次函数的图像经过点M（，n），点N（，n），交y轴于点A．

    （1）求a，b满足的关系式；

    （2）若抛物线上始终存在不重合的P，Q两点（P在Q的左边）关于原点对称．

    ①求a的取值范围；

    ②若点A，P，Q三点到直线l:的距离相等，求线段PQ长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体，并用流量、速度、密度三个概念描述车流的基本特征，其中流量q（辆/小时）指单位时间内通过道路指定断面的车辆数；速度v（千米/小时）指通过道路指定断面的车辆速度，密度k（辆/千米）指通过道路指定断面单位长度内的车辆数．

    为配合大数据治堵行动，测得某路段流量q与速度v之间关系的部分数据如下表：

    速度v（千米/小时）

    ……

    5

    10

    20

    32

    40

    48

    ……

    流量q（辆/小时）

    ……

    550

    1000

    1600

    1792

    1600

    1152

    ……

    （1）根据上表信息，下列三个函数关系式中，刻画q，v关系最准确的是___________．（只填上正确答案的序号）

    ①q=90v+100；②q=；③q=2v2+120v．

    （2）请利用（1）中选取的函数关系式分析，当该路段的车流速度为多少时，流量达到最大？最大流量是多少？

    （3）已知q，v，k满足q=vk，请结合（1）中选取的函数关系式继续解决下列问题．

    ①市交通运行监控平台显示，当18≤v≤28该路段不会出现交通拥堵现象．试分析当车流密度k在什么范围时，该路段不会出现交通拥堵现象；

    ②在理想状态下，假设前后两车车头之间的距离d（米）均相等，当d=25米时请求出此时的速度v．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为弧BE的中点，连接AD交OE于点F，若AC=FC

    （Ⅰ）求证：AC是⊙O的切线；

    （Ⅱ）若BF=5，DF=，求⊙O的半径．

    查看答案和解析>>

    同步练习册答案