
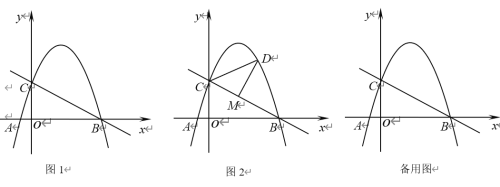
【题目】如图1,抛物线![]() 过点A(-1,0),B(4,0),与y轴相交于点C.
过点A(-1,0),B(4,0),与y轴相交于点C.
(1)求抛物线的解析式;
(2)在x轴正半轴上存在点E,使得△BCE是等腰三角形,请求出点E的坐标;
(3)如图2,点D是直线BC上方抛物线上的一个动点.过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,请求出点D的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,2或
;(3)存在,2或![]()
【解析】
(1)根据点A,B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,结合点B的坐标可得出BC的长,设点E的坐标为(m,0),分BE=BC及CE=BE两种情况考虑:①当BE=BC时,由BE=2![]() 结合点B的坐标可得出点E的坐标;②当CE=BE时,在Rt△OCE中利用勾股定理可得出关于m的一元一次方程,解之即可得出m的值,进而可得出点E的坐标;
结合点B的坐标可得出点E的坐标;②当CE=BE时,在Rt△OCE中利用勾股定理可得出关于m的一元一次方程,解之即可得出m的值,进而可得出点E的坐标;
(3)分∠DCM=2∠ABC及∠CDM=2∠ABC两种情况考虑:①当∠DCM=2∠ABC时,取点F(0,-2),连接BF,则CD∥BF,由点B,F的坐标,利用待定系数法可求出直线BF,CD的解析式,联立直线CD及抛物线的解析式成方程组,通过解方程组可求出点D的坐标;②当∠CDM=2∠ABC时,过点C作CN⊥BF于点N,作点N关于BC的对称点P,连接NP交BC于点Q,利用待定系数法及垂直的两直线一次项系数乘积为-1可求出直线CN的解析式,联立直线BF及直线CN成方程组,通过解方程组可求出点N的坐标,利用对称的性质可求出点P的坐标,由点C、P的坐标,利用待定系数法可求出直线CP的解析式,将直线CP的解析式代入抛物线解析式中可得出关于x的一元二次方程,解之取其非零值可得出点D的横坐标.综上,此题得解.
解:(1). ∵抛物线![]() 过点
过点![]() ,
,![]() ,
,
∴![]()
解得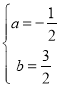
∴二次函数的表达式为:![]()
(2)抛物线![]() ,
,
当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() ;
;
∴![]() ,
,![]() ,
,![]()
∴,
![]()
![]()
①当![]() 时,如图1,
时,如图1,![]() 点是线段
点是线段![]() 的中垂线与
的中垂线与![]() 轴的交点,
轴的交点,
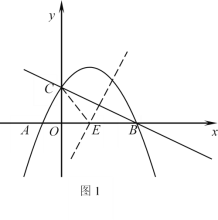
设![]() ,则
,则![]() ,在RT△OCE中,
,在RT△OCE中,
![]() ,解得
,解得![]() ,
,
∴![]()
②当![]() 时,
时, ![]()
∴![]()
(3)分两种情况考虑:
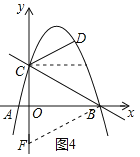
①当∠DCM=2∠ABC时,取点F(0,-2),连接BF,如图4所示.
∵OC=OF,OB⊥CF,
∴∠ABC=∠ABF,
∴∠CBF=2∠ABC.
∵∠DCB=2∠ABC,
∴∠DCB=∠CBF,
∴CD∥BF.
∵点B(4,0),F(0,-2),
∴直线BF的解析式为y=![]() x-2,
x-2,
∴直线CD的解析式为y=![]() x+2.
x+2.
联立直线CD及抛物线的解析式成方程组,得: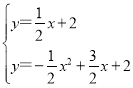 ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴点D的坐标为(2,3);
②当∠CDM=2∠ABC时,过点C作CN⊥BF于点N,作点N关于BC的对称点P,连接NP交BC于点Q,如图5所示.
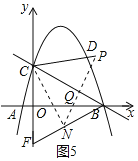
设直线CN的解析式为y=kx+c(k≠0),
∵直线BF的解析式为y=![]() x-2,CN⊥BF,
x-2,CN⊥BF,
∴k=-2.
又∵点C(0,2)在直线CN上,
∴直线CN的解析式为y=-2x+2.
连接直线BF及直线CN成方程组,得: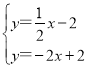 ,
,
解得: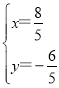 ,
,
∴点N的坐标为(![]() ).
).
∵点B(4,0),C(0,2),
∴直线BC的解析式为y=-![]() x+2.
x+2.
∵NP⊥BC,且点N(![]() ),
),
∴直线NP的解析式为y=2x-![]() .
.
联立直线BC及直线NP成方程组,得: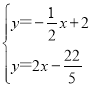 ,
,
解得: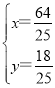 ,
,
∴点Q的坐标为(![]() ).
).
∵点N(![]() ),点N,P关于BC对称,
),点N,P关于BC对称,
∴点P的坐标为(![]() ).
).
∵点C(0,2),P(![]() ),
),
∴直线CP的解析式为y=![]() x+2.
x+2.
将y=![]() x+2代入y=-
x+2代入y=-![]() x+2整理,得:11x2-29x=0,
x+2整理,得:11x2-29x=0,
解得:x1=0(舍去),x2=![]() ,
,
∴点D的横坐标为![]() .
.
综上所述:存在点D,使得△CDM的某个角恰好等于∠ABC的2倍,点D的横坐标为2或![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】“只要人人都献出一点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂捐款”活动倡议,有2500名居民踊跃参与献爱心.社区管理员随机抽查了部分居民捐款情况,统计图如图:

(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人?
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=3,BC=1,点D是斜边上一点,且AD=4BD.
(1)求tan∠BCD的值;
(2)过点B的⊙O与边AC相切,切点为AC的中点E,⊙O与直线BC的另一个交点为F.
(ⅰ)求⊙O的半径;
(ⅱ) 连接AF,试探究AF与CD的位置关系,并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小米先从盒子中随机取出一个小球,记下数字为x,且不放回盒子,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小米、小华各取一次小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加一个知识竞赛,该竞赛试题由10道选择题构成,每小题有四个选项,且只有一个选项正确.其给分标准为:答对一题得2分,答错一题扣1分,不答得0分,若10道题全部答对则额外奖励5分.小明对其中的8道题有绝对把握答对,剩下2道题完全不知道该选哪个选项.
(1)对于剩下的2道题,若小明都采用随机选择一个选项的做法,求两小题都答错的概率;
(2)从预期得分的角度分析,采用哪种做法解答剩下2道题更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
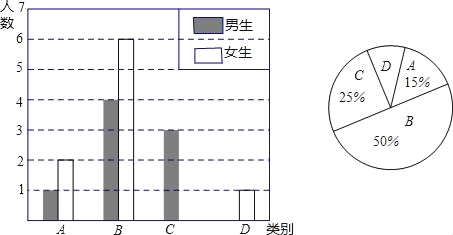
【题目】李老师为了了解班级学生自主学习、合作交流的具体情况,对九(1)班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C;一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图.请你根据统计图解答下列问题:
(1)本次调查中,李老师一共调查了 名同学,其中女生共有 名.
(2)将上面的条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请求所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在疫情期间用3000元购进A、B两种口罩1100个,购买A种口罩与购买B种口罩的费用相同,且A种口罩的单价是B种口罩单价的1.2倍;
(1)求A,B两种口罩的单价各是多少元?
(2)若计划用不超过7000元的资金再次购进A、B两种口罩共2600个,已知A、B两种口罩的进价不变,求A种口罩最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某学校高中两个班的学生上学时步行、骑车、乘公交、乘私家车人数的扇形统计图,已知乘公交人数是乘私家车人数的2倍.若步行人数是18人,则下列结论正确的是( )

A. 被调查的学生人数为90人
B. 乘私家车的学生人数为9人
C. 乘公交车的学生人数为20人
D. 骑车的学生人数为16人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com