
【题目】在新冠疫情防控期间,某医疗器械商业集团新进了40台A型电子体温测量仪,60台B型电子体温测量仪,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种测量仪每台的利润(元)如下表:
A型 | B型 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店![]() 台A型测量仪,集团卖出这100台测量仪的总利润为
台A型测量仪,集团卖出这100台测量仪的总利润为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围:
的取值范围:
(2)为了促销,集团决定仅对甲连锁店的A型测量仪每台让利![]() 元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大?
元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大?
【答案】(1)![]() (10≤
(10≤![]() ≤40);(2)当0<
≤40);(2)当0<![]() <20时,调配给甲连锁店A型40台,B型30台,乙连锁店A型 0台,B型30台;当
<20时,调配给甲连锁店A型40台,B型30台,乙连锁店A型 0台,B型30台;当![]() =20时,所有方案利润相同; 当20<
=20时,所有方案利润相同; 当20<![]() <30时,调配给甲连锁店A型10台,B型60台,乙连锁店A型 30台,B型0台
<30时,调配给甲连锁店A型10台,B型60台,乙连锁店A型 30台,B型0台
【解析】
(1)首先设调配给甲连锁店![]() 台A型测量仪,则调配给甲连锁店B型测温仪
台A型测量仪,则调配给甲连锁店B型测温仪![]() 台,调配给乙连锁店A型测温仪
台,调配给乙连锁店A型测温仪![]() 台,B型
台,B型![]() 台,根据题意列出函数关系式,列出不等式组求出
台,根据题意列出函数关系式,列出不等式组求出![]() 的取值范围即可;
的取值范围即可;
(2)依题意得出y与a的关系式,解出不等式方程后可得出使利润达到最大的分配方案.
解:(1)根据题意知,调配给甲连锁店B型测温仪![]() 台,调配给乙连锁店A型测温仪
台,调配给乙连锁店A型测温仪![]() 台,B型
台,B型![]() 即
即![]() 台,
台,
![]() .
.
即![]() .
.
∵ ,
,
∴10≤![]() ≤40.
≤40.
∴![]() (10≤
(10≤![]() ≤40);
≤40);
(2)由题意知![]() ,
,
即![]() .
.
∵![]() >170,
>170,
∴![]() <30,
<30,
当0<![]() <20时,当
<20时,当![]() =40时,总利润达到最大,即调配给甲连锁店A型40台,B型30台,乙连锁店A型 0台,B型30台;
=40时,总利润达到最大,即调配给甲连锁店A型40台,B型30台,乙连锁店A型 0台,B型30台;
当![]() =20时,
=20时,![]() 的取值在10≤
的取值在10≤![]() ≤40内时所有方案利润相同;
≤40内时所有方案利润相同;
当20<![]() <30时,当
<30时,当![]() =10时,总利润达到最大,即调配给甲连锁店A型10台,B型60台,乙连锁店A型 30台,B型0台.
=10时,总利润达到最大,即调配给甲连锁店A型10台,B型60台,乙连锁店A型 30台,B型0台.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中
中![]() ,点
,点![]() 从点
从点![]() 运动到点
运动到点![]() 停止,连接
停止,连接![]() ,以
,以![]() 长为直径作
长为直径作![]() .
.
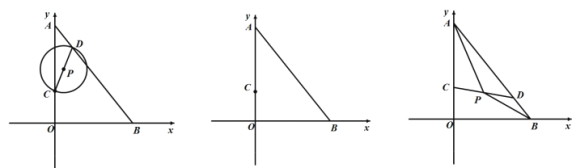
(1)若![]() ,求
,求![]() 的半径;
的半径;
(2)当![]() 与
与![]() 相切时,求
相切时,求![]() 的面积;
的面积;
(3)连接![]() ,在整个运动过程中,
,在整个运动过程中,![]() 的面积是否为定值,如果是,请直接写出面积的定值,如果不是,请说明理由.
的面积是否为定值,如果是,请直接写出面积的定值,如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 在
在![]() 上取两点
上取两点![]() (
(![]() 在
在![]() 左边),以
左边),以![]() 为边作等边三角形
为边作等边三角形![]() ,使顶点
,使顶点![]() 在
在![]() 上,
上,![]() 分别交
分别交![]() 于点
于点![]() .
.
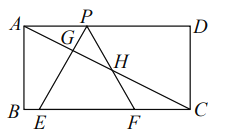
(1)求![]() 的边长;
的边长;
(2)在不添加辅助线的情况下,当![]() 与
与![]() 不重合时,从图中找出一对相似三角形,并说明理由;
不重合时,从图中找出一对相似三角形,并说明理由;
(3)若![]() 的边
的边![]() 在线段
在线段![]() 上移动.试猜想:
上移动.试猜想:![]() 与
与![]() 有何数量关系?并证明你猜想的结论.
有何数量关系?并证明你猜想的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() +bx+c经过△ABC的三个顶点,其中点A(0,﹣1),点B(9,﹣10),AC∥x轴,点P是直线AC上方抛物线上的动点.
+bx+c经过△ABC的三个顶点,其中点A(0,﹣1),点B(9,﹣10),AC∥x轴,点P是直线AC上方抛物线上的动点.
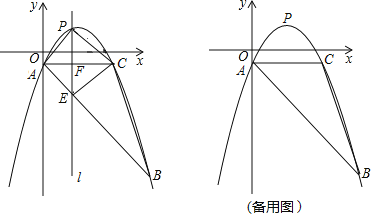
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形 图中区域 | D | E | C |

(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“只要人人都献出一点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂捐款”活动倡议,有2500名居民踊跃参与献爱心.社区管理员随机抽查了部分居民捐款情况,统计图如图:

(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人?
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
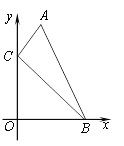
【题目】如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com