
【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如表:

已知该运动服的进价为每件150元.
(1)售价为x元,月销量为y件.
①求y关于x的函数关系式:
②若销售该运动服的月利润为w元,求w关于x的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了a元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则a的值是多少?
【答案】(1)①![]() ;②
;②![]() 元;(2)30元
元;(2)30元
【解析】
(1)①设y关于x的函数关系式为y=kx+b,由待定系数法求解即可;
②月利润w=(x-150)(-2x+600),整理并配方,然后根据二次函数的性质可得答案;
(2)设调整后的售价为t元,则调整后的单件利润为(t-150+a)元,销量为(-2t+600)件,写出月利润关于x的函数,并根据二次函数的性质得出月利润最大时的t值,从而得出关于a的方程,解出a即可.
解:(1)①设y关于x的函数关系式为y=kx+b,把(200,200),(210,180)
代入得:![]()
解得:![]() ,
,
∴y关于x的函数关系式为y=-2x+600;
②月利润w=(x﹣150)(﹣2x+600)=﹣2x2+900x﹣90000
=﹣2(x﹣225)2+11250.
∵﹣2<0,
∴w为开口向下的抛物线,
∴当x=225时,月最大利润为11250元;
∴w关于x的函数关系式为w=﹣2x2+900x﹣90000,月利润最大时的售价为225元;
(2)设调整后的售价为t元,则调整后的单件利润为(t﹣150+a)元,销量为(﹣2t+600)件.
月利润w=(t﹣150+a)(﹣2t+600)
=﹣2t2+(900﹣2a)t+600a﹣90000,
∴当![]() 时,月利润最大,则
时,月利润最大,则![]() =210,
=210,
解得a=30.
∴a的值是30元.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】解不等式组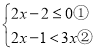
请结合题意填空,完成本题的解答
(1)解不等式①,得___________;
(2)解不等式②,得___________;
(3)把不等式①和②的解集在数轴上表示出来:
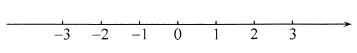
(4)原不等式组的解集为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为l的方格纸中,有线段AB,BC.点A,B,C均在小正方形的顶点上.
(1)在图1中画出四边形ABCD,四边形ABCD是轴对称图形,点D在小正方形的项点上:
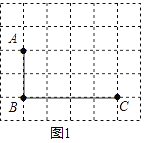
(2)在图2中画四边形ABCE,四边形ABCE不是轴对称图形,点E在小正方形的项点上,∠AEC=90°,EC>EA;直接写出四边形ABCE的面积为________.
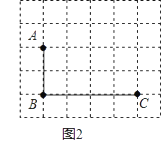
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市特产大闸蟹,2016年的销售额是![]() 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达
亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达![]() 亿元,若2017、2018年每年销售额增加的百分率都相同.
亿元,若2017、2018年每年销售额增加的百分率都相同.
(1)求平均每年销售额增加的百分率;
(2)该市这![]() 年大闸蟹的总销售额是多少亿元?
年大闸蟹的总销售额是多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8,点E是AB的中点,以AE为边作等边△ADE(点D与点C分别在AB异侧),连接CD,则△ACD的面积是_________.
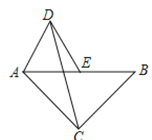
查看答案和解析>>
科目:初中数学 来源: 题型:
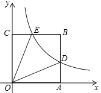
【题目】平面直角坐标系中,正方形OABC如图放置,反比例函数![]() 的图像交AB于点D,交BC于点E,已知A(
的图像交AB于点D,交BC于点E,已知A(![]() ,0),∠DOE=30°,则k的值为( )
,0),∠DOE=30°,则k的值为( )
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示直线y=kx+2(k≠0)与反比例函数y=![]() (m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=
(m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=![]() ,过P点作x轴的垂线交于点C,连接AC,
,过P点作x轴的垂线交于点C,连接AC,
(1)求一次函数的解析式.
(2)若AC是△PCB的中线,求反比例函数的关系式.
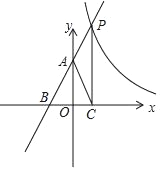
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直x=1线,下列结论中:①abc>0;②若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;③若方程a(x+2)(4﹣x)=﹣2的两根为x1,x2,且x1<x2,则﹣2<x1<x2<4;④(a+c)2>b2;一定正确的是______(填序号即可).
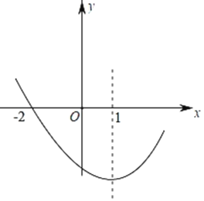
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com