
【题目】如图,在△ABC中,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
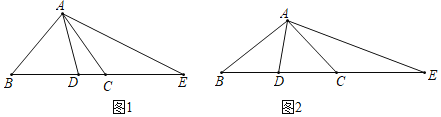
(1)若∠BAC=90°(图1),求∠DAE的度数;
(2)若∠BAC=120°(图2),求∠DAE的度数;
(3)当∠BAC>90°时,探求∠DAE与∠BAC之间的数量关系,直接写出结果.
【答案】(1)∠DAE=45°,(2)∠DAE=60°;(3)∠DAE=![]() ∠BAC
∠BAC
【解析】
(1)由于AB=AC,∠BAC=90°,从而求出∠B=∠ACB=45°,又因为BD=BA,可知∠BAD=∠BDA=67.5°,因为CE=CA,可知∠CAE=∠E=![]() ∠ACB=22.5°,最后可求出得∠DAE=∠BAE﹣∠BAD=45°.
∠ACB=22.5°,最后可求出得∠DAE=∠BAE﹣∠BAD=45°.
(2)由于AB=AC,∠BAC=120°,从而求出∠B=∠ACB=30°,又因为BD=BA,可知∠BAD=∠BDA=75°,因为CE=CA,可知∠CAE=∠E=![]() ∠ACB=15°,最后可求出得∠DAE=∠BAE﹣∠BAD=60°.
∠ACB=15°,最后可求出得∠DAE=∠BAE﹣∠BAD=60°.
(3)可设∠CAE=x,∠BAD=y,则∠B=180°﹣2y,∠E=∠CAE=x,从而可知∠BAE=2y﹣x,∠DAE=y﹣x,∠BAC=2y﹣2x,所以可知∠DAE=![]() ∠BAC,
∠BAC,
(1)如图1,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180°﹣∠B)=67.5°,
(180°﹣∠B)=67.5°,
∵CE=CA
∴∠CAE=∠E=![]() ∠ACB=22.5°,
∠ACB=22.5°,
∴∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=45°,
(2)如图2,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=30°,
∵BA=BD,
∴∠BAD=∠BDA=75°,
∴∠DAC=45°,
∵CA=CE,
∴∠E=∠CAE=15°,
∴∠DAE=∠DAC+∠CAE=60°;
(3)∠DAE=![]() ∠BAC,
∠BAC,
理由:设∠CAE=x,∠BAD=y,
则∠B=180°﹣2y,∠E=∠CAE=x,
∴∠BAE=180°﹣∠B﹣∠E=2y﹣x,
∴∠DAE=∠BAE﹣∠BAD=2y﹣x﹣y=y﹣x,
∠BAC=∠BAE﹣∠CAE=2y﹣x﹣x=2y﹣2x
∴∠DAE=![]() ∠BAC.
∠BAC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,点E,F分别在边BCCD上,BE=CF=1,小球P从点E出发沿直线向点F运动,完成第1次与边的碰撞,每当碰到正方形的边时反弹,反弹时反射角等于入射角,则小球P与正方形的边第2次碰撞到__边上,小球P与正方形的边完成第5次碰撞所经过的路程为__.
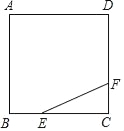
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团去景点游览,共有成人和儿童20人,且旅行团中儿童人数多于成人.景点规定:成人票40元/张,儿童票20元/张.
(1)若20人买门票共花费560元,求成人和儿童各多少人?
(2)景区推出“庆元旦”优惠方案,具体方案为:
方案一:购买一张成人票免一张儿童票费用;
方案二:成人票和儿童票都打八折优惠;
设:旅行团中有成人a人,旅行团的门票总费用为W元.
①方案一:![]() _____________________;
_____________________;
方案二:![]() ____________________;
____________________;
②试随着a的变化,哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成。
(1)若围成的面积为180m2,试求出自行车车棚的长和宽;
(2)能围成的面积为200m2自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,我们在2018年某月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”)该十字星的十字差为![]() ,再选择其它位置的十字星,可以发现“十字差”仍为48.
,再选择其它位置的十字星,可以发现“十字差”仍为48.
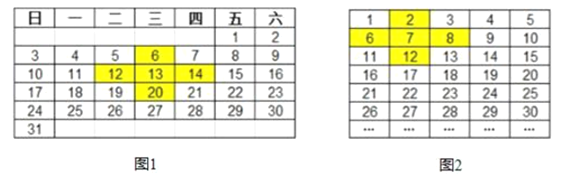
(1)如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为 .
(2)若将正整数依次填入6列的长方形数表中,不同位置十字星的“十字差”是一个定值吗?如果是,请求出这个定值;如果不是,请说明理由.
(3)若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数![]() 有关的定值,请用
有关的定值,请用![]() 表示出这个定值,并证明你的结论.
表示出这个定值,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,分别交m、n于点A、B,当点B与点D重合时(如图1),连结PA,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图1的情况下,把直线l向右平移到如图2的位置,试问(1)中的PA与PB
的关系式是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(3)延伸探究:在图2的情况下,把直线l绕点A旋转,使得∠APB=90°(如图3),若两平行线m、n之间的距离为2k,求证:PAPB=kAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
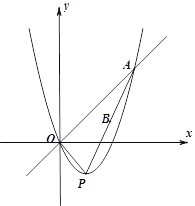
【题目】如图,已知直线![]() 与二次函数
与二次函数![]() 的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=
的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=![]() ,AP的中点为B.
,AP的中点为B.
(1)求二次函数的解析式;
(2)求线段OB的长;
(3)若射线OB上存在点Q,使得△AOQ与△AOP相似,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com