
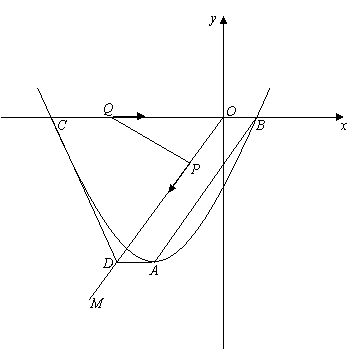
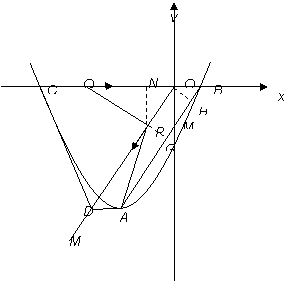
如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式、直线AB的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿着射线OM运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.
问题一:当t为何值时△OPQ为等腰三角形;
问题二:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
 |
解:(1)∴y=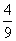 (x+2)2-4,或y=
(x+2)2-4,或y=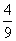 x2+
x2+ x-
x-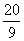 ;y=
;y=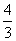 x—
x—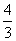 .
.
(2)问题一: 、
、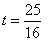 、
、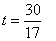

问题二:将y=0代入y=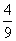 x2+
x2+ x-
x-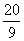 ,得
,得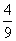 x2+
x2+ x-
x-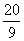 =0,解得x=1或-5.
=0,解得x=1或-5.
∴C(-5,0).∴OC=5.
∵OM∥AB, AD∥x轴,∴四边形ABOD是平行四边形.
∴AD=OB=1.∴点D的坐标是(-3,-4).
∴S△DOC=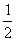 ×5×4=10.
×5×4=10.
过点P作PN⊥BC,垂足为N.易证△OPN∽△BOH.
∴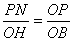 ,即
,即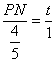 .∴PN=
.∴PN= t.
t.
∴四边形CDPQ的面积S=S△DOC-S△OPQ=10-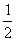 ×(5-2t )×
×(5-2t )× t=
t= t2-2 t +10.
t2-2 t +10.
∴当 t=
t=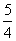 时,四边形CDPQ的面积S最小.
时,四边形CDPQ的面积S最小.
此时,点P的坐标是(-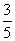 ,-1),点Q的坐标是(-
,-1),点Q的坐标是(-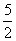 ,0),
,0),
∴PQ=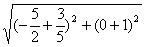 =
=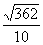 .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飞行的小鸟,将随意地落在图中所示的方格地面上,求小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪,则编号为1、2的2个小方格空地种
植草坪的概率是多少(用树状图或列表法求解)?

查看答案和解析>>
科目:初中数学 来源: 题型:
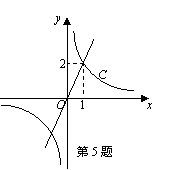
反比例函数y﹦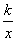 和正比例函数y﹦mx的图象如图所示.由此可以得到方程
和正比例函数y﹦mx的图象如图所示.由此可以得到方程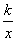 ﹦mx的实数根为 ( )
﹦mx的实数根为 ( )
A.x﹦1 B.x﹦2 C.x1﹦1,x2﹦-1 D.x1﹦1,x2﹦-2
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
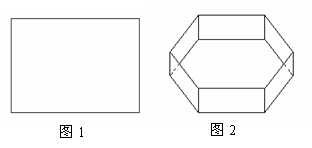
动手实验:利用矩形纸片(图1)剪出一个正六边形纸片;利用这个正六边形纸片做一个如图(2)无盖的正六棱柱(棱柱底面为正六边形);
(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2)在(1)的前提下,当矩形的长为2 时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率?(矩形纸片的利用率=
时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率?(矩形纸片的利用率= 无盖正六棱柱的表面积/矩形纸片的面积)
无盖正六棱柱的表面积/矩形纸片的面积)
 |  | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com