
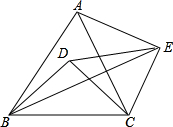
 如图,△ABC和△EDC都是正三角形,连接BD、AE、BE,若∠AEB=45°,则∠DEB等于( )
如图,△ABC和△EDC都是正三角形,连接BD、AE、BE,若∠AEB=45°,则∠DEB等于( )| A、15° | B、20° |
| C、25° | D、30° |
|


科目:初中数学 来源: 题型:
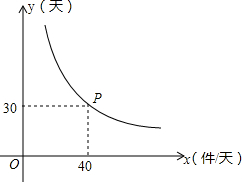 问题情境:为了提高产品的技术含量,我省某贸易公司计划把研发的一批新产品精加工后再投放市场,加工所需时间y(单位:天)与平均每天的工作量x(单位:件/天)之间的关系是我们学过的某种函数,其图象如图所示.
问题情境:为了提高产品的技术含量,我省某贸易公司计划把研发的一批新产品精加工后再投放市场,加工所需时间y(单位:天)与平均每天的工作量x(单位:件/天)之间的关系是我们学过的某种函数,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
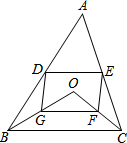 D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、151人 | B、141人 |
| C、131人 | D、105人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com