【题目】如图，将矩形
绕点
顺时针旋转到矩形
的位置，旋转角为
（
），若
，则
的大小是（ ）
A.
B.
C.
D.
【答案】A
【解析】
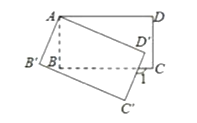
根据矩形的性质得∠BAD=∠ABC=∠ADC=90°，再根据旋转的性质得∠BAB′=α，∠B′AD′=∠BAD=90°，∠D′=∠D=90°，然后根据四边形的内角和得到∠3=68°，再利用互余即可得到∠α的大小．
解：∵四边形ABCD为矩形，
∴∠BAD=∠ABC=∠ADC=90°，
∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α，
∴∠BAB′=α，∠B′AD′=∠BAD=90°，∠AD′C′=∠ADC=90°，
∵∠2=∠1=112°，
而∠ABC=∠D′=90°，
∴∠3=180°-∠2=68°，
∴∠BAB′=90°-68°=22°，
即∠α=22°．
故选：A．
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H，给出下列结论：①BE=2AE；②△DFP∽△BPH；③△PFD∽△PDB；④DP2=PHPC
其中正确的是（ ）
A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．
（1）证明：DF是⊙O的切线；
（2）若AC＝3AE，FC＝6，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．
（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是 ；
（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是 ；
（3）△A2B2C2的面积是 平方单位．
查看答案和解析>>
科目：初中数学 来源： 题型：
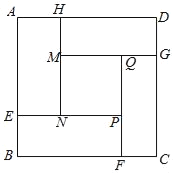
【题目】创客联盟的队员想用3D打印完成一幅边长为6米的正方形作品ABCD，设计图案如图所示（四周阴影是四个全等的矩形，用材料甲打印；中心区是正方形MNPQ，用材料乙打印）．在打印厚度保持相同的情况下，两种材料的消耗成本如下表：
材料 | 甲 | 乙 |
价格（元/米2） | 80 | 50 |
设矩形的较短边AH的长为x米，打印材料的总费用为y元．
（1）MQ的长为 米（用含x的代数式表示）；
（2）求y关于x的函数解析式；
（3）当中心区的边长不小于2米时，预备材料的购买资金2800元够用吗？请利用函数的增减性来说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
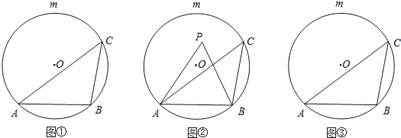
【题目】如图①,AB是圆O的一条弦,点C是优弧
上一点.
(1)若∠ACB=45°,点P是O上一点(不与A.B重合)，则∠APB=___；
(2)如图②,若点P是弦AB与所围成的弓形区域(不含弦AB与)内一点.求证：∠APB>∠ACB；
(3)请在图③中直接用阴影部分表示出在弦AB与所围成的弓形区域内满足
的点P所在的范围；
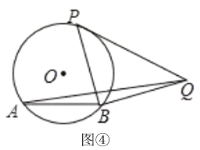
（4）在（1）的条件下，以PB为边，向右作等腰直角三角形PBQ，连结AQ，如图4，已知AB=2，
①当点Q在线段AB的延长线上时，线段AQ的长为____________
②线段AQ的最小值为_____________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．
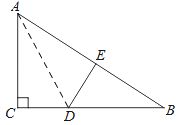
（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知正方形ABCD的边长为6，E，F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．
(1)求证：EF=MF；
(2)若AE=2，求FC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
