
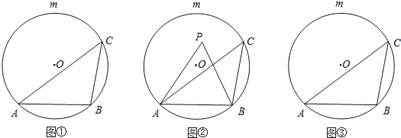
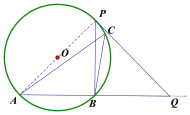
【题目】如图①,AB是圆O的一条弦,点C是优弧![]() 上一点.
上一点.
(1)若∠ACB=45°,点P是O上一点(不与A.B重合),则∠APB=___;
(2)如图②,若点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;
(3)请在图③中直接用阴影部分表示出在弦AB与![]() 所围成的弓形区域内满足
所围成的弓形区域内满足
![]() 的点P所在的范围;
的点P所在的范围;
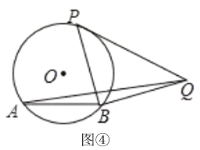
(4)在(1)的条件下,以PB为边,向右作等腰直角三角形PBQ,连结AQ,如图4,已知AB=2,
①当点Q在线段AB的延长线上时,线段AQ的长为____________
②线段AQ的最小值为_____________
【答案】(1)45°或135°;(2)答案见详解;(3)答案见详解;(4)① 4;②![]()
【解析】
(1)根据题意,点P在优弧![]() 上时,∠APB=∠ACB=45°;当点P在劣弧
上时,∠APB=∠ACB=45°;当点P在劣弧![]() 上时,∠APB=180°-∠ACB=135°;
上时,∠APB=180°-∠ACB=135°;
(2)延长AP交圆O于点Q,连接BQ,根据三角形的外角大于任何一个与它不相邻的内角,可以得证;
(3)根据第(2)问和圆周角定理可知,画出过点A、B、O的圆,即可得到点P所在的阴影部分;
(4)①根据题意可知,![]() 是等腰直角三角形,点Q在线段AB的延长线上时,点P只能在优弧
是等腰直角三角形,点Q在线段AB的延长线上时,点P只能在优弧![]() 上,且
上,且![]() ,证明
,证明![]() 是等腰直角三角形即可得解;
是等腰直角三角形即可得解;
②根据题意,连接PA,设PQ交![]() 于点T,连接AT,BT,可得AT是
于点T,连接AT,BT,可得AT是 ![]() 的直径,即
的直径,即![]() 是等腰直角三角形,AB=BT=2,以BT为底向右作等腰RtBKT,则KT=KB=
是等腰直角三角形,AB=BT=2,以BT为底向右作等腰RtBKT,则KT=KB=![]() ,由∠BQT=45°,可得点Q的运动轨迹是以K为圆心,KT为半径的圆;求出AK的值为
,由∠BQT=45°,可得点Q的运动轨迹是以K为圆心,KT为半径的圆;求出AK的值为![]() ,最后根据三角形三边长的关系,即可得到AQ的最小值.
,最后根据三角形三边长的关系,即可得到AQ的最小值.
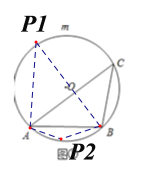
(1)如图①所示,
第一种情况:点P在优弧![]() 上时,∠AP1B=∠ACB=45°;
上时,∠AP1B=∠ACB=45°;
第二种情况:点P在劣弧![]() 上时,
上时,
∵四边形ACBP2是圆的内接四边形,
∴![]()
∴∠AP2B=180°-∠ACB=135°,
故答案为:45°或135°;
(2)如图②所示,延长AP交圆O于点Q,连接BQ,则![]() ,
,
∵![]()
∴∠APB>∠PQB,即∠APB>∠ACB;

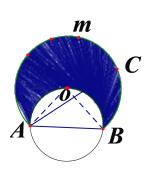
(3)连接AO,BO,作![]() 的外接圆,即可得到所求的阴影部分;
的外接圆,即可得到所求的阴影部分;
(4)①如图:
∵![]() 是等腰直角三角形,点Q在线段AB的延长线上,
是等腰直角三角形,点Q在线段AB的延长线上,
∴点P只能在优弧![]() 上,且
上,且![]() ,
,
连接AP,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ;
;
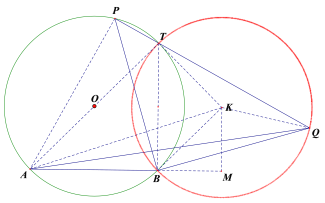
②如图,连接PA,设PQ交![]() 于点T,连接AT,BT.
于点T,连接AT,BT.
∵∠APB=∠BPQ=45°,
∴∠APT=90°,
∵∠TAB=∠BPQ=45°,∠ABT=90°,
∴AB=BT=2,
以BT为底边向右作等腰RtBKT,则KT=KB=![]() ,
,
∵∠BQT=45°,
∴点Q的运动轨迹是以K为圆心,KT为半径的圆,KQ=KT=KB=![]()
作KM⊥BA交AB的延长线于点M,连接AK,MB=KM=1,AM=3,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴AQ的最小值是![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
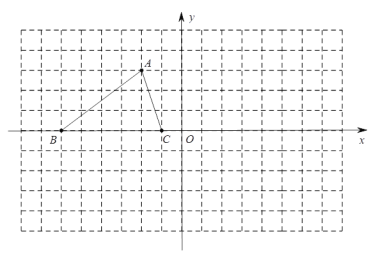
(1)点A关于y轴对称的点的坐标是 ;
(2)将△ABC绕坐标原点O顺时针旋转180°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
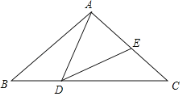
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=![]() ,DE交AC于点E,若△DCE为直角三角形,则BD的值为_______.
,DE交AC于点E,若△DCE为直角三角形,则BD的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.

(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角板OMN绕点O按每秒30°的速度按逆时针方向旋转一周,在旋转的过程中,在第____________秒时,直线MN恰好与直线CD垂直.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆
O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
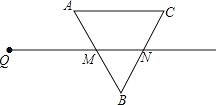
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
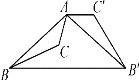
A. 55°B. 65°C. 85°D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,我们来进行以下的探索:
)2,我们来进行以下的探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,这样就得出了把类似a+b
,∴a=m2+2n2,b=2mn,这样就得出了把类似a+b![]() 的式子化为平方式的方法,请仿照上述方法探索并解决下列问题:
的式子化为平方式的方法,请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a= ,b= .
)2,用含m,n的式子分别表示a,b,得a= ,b= .
(2)若a﹣4![]() =(m﹣n
=(m﹣n![]() )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com