
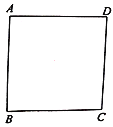
【题目】已知:正方形![]() ,
,![]() 为平面内任意一点,连接
为平面内任意一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,当点
,当点![]() ,
,![]() ,
,![]() 在一条直线时,若
在一条直线时,若![]() ,
,![]() ,则
,则![]() ________.
________.
【答案】![]() 或
或![]()
【解析】
分两种情况讨论:
(1)当点G在线段BD上时,如下图连接EG交CD于F;(2)当点G在线段BD的延长线上时,如下图连接EG交CD的延长线于F.根据两种情况分别画出图形,证得![]() 是等腰直角三角形,求出DF=EF=2,然后在直角三角形ECF中利用勾股定理即可求出CE的长.
是等腰直角三角形,求出DF=EF=2,然后在直角三角形ECF中利用勾股定理即可求出CE的长.
解:分两种情况讨论:
(1)当点G在线段BD上时,如下图连接EG交CD于F
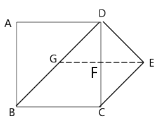
∵ABCD是正方形
∴CD=AD=4
∵线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]()
∴![]() 是等腰直角三角形,DE=DG=
是等腰直角三角形,DE=DG= ![]()
∴DF=EF=2
∴CF=CD-DF=4-2=2
∴CE=![]()
(2)当点G在线段BD的延长线上时,如下图连接EG交CD的延长线于F
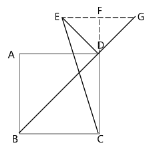
∵ABCD是正方形
∴CD=AD=4
∵线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]()
∴![]() 是等腰直角三角形,DE=DG=
是等腰直角三角形,DE=DG= ![]()
∴DF=EF=2
∴CF=CD+DF=4+2=6
∴CE=![]()
综上所述,CE的长为![]() 或
或![]()


科目:初中数学 来源: 题型:
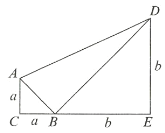
【题目】如图,已知等腰直角三角形![]() 的边
的边![]() ,等腰直角三角形
,等腰直角三角形![]() 的边
的边![]() ,且
,且![]() ,点
,点![]() 、
、![]() 、
、![]() 放置在一条直线上,联结
放置在一条直线上,联结![]() .
.
(1)求三角形![]() 的面积;
的面积;
(2)如果点![]() 是线段
是线段![]() 的中点,联结
的中点,联结![]() 、
、![]() 得到三角形
得到三角形![]() ,求三角形
,求三角形![]() 的面积;
的面积;
(3)第(2)小题中的三角形![]() 与三角形
与三角形![]() 面积哪个较大?大多少?(结果都可用
面积哪个较大?大多少?(结果都可用![]() 、
、![]() 代数式表示,并化简)
代数式表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在下列关系中,不属于直角三角形的是( )
A. b2=a2﹣c2 B. a:b:c=3:4:5
C. ∠A﹣∠B=∠C D. ∠A:∠B:∠C=3:4:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,王同学使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为![]() ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图![]() 为2002年世界数学家大会的会标,它是用四个形状相同、大小相等的直角三角形拼成的正方形,请通过图形的运动,在右侧网格中补全此会标.
为2002年世界数学家大会的会标,它是用四个形状相同、大小相等的直角三角形拼成的正方形,请通过图形的运动,在右侧网格中补全此会标.
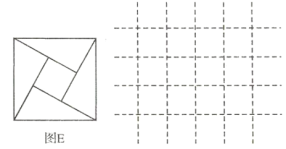
(1)问此正方形会标是旋转对称图形吗?答:______.
(2)若会标中直角三角形的两条直角边长分别为![]() 和
和![]() ,请用含
,请用含![]() (其中
(其中![]() )的代数式表示出此正方形会标的面积.
)的代数式表示出此正方形会标的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
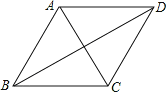
A. △ABD与△ABC的周长相等
B. △ABD与△ABC的面积相等
C. 菱形的周长等于两条对角线之和的两倍
D. 菱形的面积等于两条对角线之积的两倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() :
:![]() 与函数
与函数![]() .
.
(1)直线![]() 经过定点
经过定点![]() ,直接写出点
,直接写出点![]() 的坐标:_______;
的坐标:_______;
(2)当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象存在唯一的公共点,在图
的图象存在唯一的公共点,在图![]() 中画出
中画出![]() 的函数图象并直接写出
的函数图象并直接写出![]() 满足的条件;
满足的条件;
(3)如图![]() ,在平面直角坐标系中存在正方形
,在平面直角坐标系中存在正方形![]() ,已知
,已知![]() 、
、![]() .请认真思考函数
.请认真思考函数![]() 的图象的特征,解决下列问题:
的图象的特征,解决下列问题:
①当![]() 时,请直接写出函数
时,请直接写出函数![]() 的图象与正方形
的图象与正方形![]() 的边的交点坐标:_______;
的边的交点坐标:_______;
②设正方形![]() 在函数
在函数![]() 的图象上方的部分的面积为
的图象上方的部分的面积为![]() ,求出
,求出![]() 与
与![]() 的函数关系式.
的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两点在数轴上,点
两点在数轴上,点![]() 表示的数为-10,点
表示的数为-10,点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 距离的3倍,点
距离的3倍,点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向右运动.点
向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向右运动(点
向右运动(点![]() 、
、![]() 同时出发)
同时出发)
![]()
(1)数轴上点![]() 对应的数是______.
对应的数是______.
(2)经过几秒,点![]() 、点
、点![]() 分别到原点
分别到原点![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 村有肥料200吨,
村有肥料200吨,![]() 村有肥料300吨,现要将这些肥料全部运往
村有肥料300吨,现要将这些肥料全部运往![]() 、
、![]() 两仓库.从
两仓库.从![]() 村往
村往![]() 、
、![]() 两仓库运肥料的费用分别为每吨20元和25元;从
两仓库运肥料的费用分别为每吨20元和25元;从![]() 村往
村往![]() 、
、![]() 两仓库运肥料的费用分别为每吨15元和18元;现
两仓库运肥料的费用分别为每吨15元和18元;现![]() 仓库需要肥料240吨,现
仓库需要肥料240吨,现![]() 仓库需要肥料260吨.
仓库需要肥料260吨.
(1)设![]() 村运往
村运往![]() 仓库
仓库![]() 吨肥料,
吨肥料,![]() 村运肥料需要的费用为
村运肥料需要的费用为![]() 元;
元;![]() 村运肥料需要的费用为
村运肥料需要的费用为![]() 元.
元.
①写出![]() 、
、![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
②试讨论![]() 、
、![]() 两村中,哪个村的运费较少?
两村中,哪个村的运费较少?
(2)考虑到![]() 村的经济承受能力,
村的经济承受能力,![]() 村的运输费用不得超过4830元,设两村的总运费为
村的运输费用不得超过4830元,设两村的总运费为![]() 元,怎样调运可使总运费最少?
元,怎样调运可使总运费最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com