
����Ŀ�������ͥ��ȼ����Ϊ��ˮ������ȼ�ϣ���Լ�����������ճ������зdz���ʵ������.ij��ȼ������ťλ�ô�0�ȵ�90�ȣ�ȼ���ر�ʱ��ȼ������ťλ��Ϊ0�ȣ���ť�Ƕ�Խ��ȼ������Խ��ȼ���������ʱ����ť�Ƕ�Ϊ90��.Ϊ����ȼ������ť�ڲ�ͬλ���ϵ�ȼ������������ͬ�����£�ѡ����ȼ������ť��5����ͬλ���Ϸֱ��տ�һ��ˮ������ť�Ƕ�̫Сʱ����������ܹ���ˮ�տ�����ѡ����ť�Ƕ�![]() �ȵķ�Χ��
�ȵķ�Χ��![]() ������¼������ݵõ��±���
������¼������ݵõ��±���
��ť�Ƕȣ��ȣ� | 20 | 50 | 70 | 80 | 90 |
����ȼ���������� | 73 | 67 | 83 | 97 | 115 |
��1���������ѧϰ����һ�κ����������������Ͷ��κ�����ȷ�����ֺ����ܱ�ʾ����ȼ����![]() ������ת�Ƕ�
������ת�Ƕ�![]() �ȵı仯���ɣ�˵��ȷ�����ֺ����������������������ɣ���������Ľ���ʽ��
�ȵı仯���ɣ�˵��ȷ�����ֺ����������������������ɣ���������Ľ���ʽ��
��2������ת�Ƕ�Ϊ����ʱ���տ�һ��ˮ����ȼ�������٣������Ƕ��٣�
��3��ij��ͥʹ�ô˿�ȼ�����ǰϰ�߰�ȼ����������ֲ������ʡȼ������ת�Ƕȣ����ü�ͥ����ÿ�µ�ƽ��ȼ������Ϊ13�����ף�������ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ�����������ף�
���𰸡���1��![]() ����2������ת�Ƕ�Ϊ40��ʱ���տ�һ��ˮ����ȼ�������٣�����Ϊ65������3����ͥ����ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ��
����2������ת�Ƕ�Ϊ40��ʱ���տ�һ��ˮ����ȼ�������٣�����Ϊ65������3����ͥ����ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ��![]() ������.
������.
��������
��1���ȼ��躯��Ϊһ�κ�������ѡ���������������ʽ���ٽ����������֤���ټ��躯��Ϊ���κ�������ѡ�������������ʽ���ٽ����������֤��
��2������1��������κ�������ʽ����Ϊ����ʽ��ת��Ϊ���κ�����ֵ�����⣬���ɽ��
��3���ɣ�2��������֪���������ʡȼ������ť�Ƕ�40�ȱȰ�ȼ���������ʱ�տ�һ��ˮ��Լ����115-65-50������ü�ͥ��ǰÿ��ƽ��������Ϊa�����ף��ݴ˽��.
�⣺��1���ټ���仯����Ϊһ�κ���![]() ��
��![]()
����20��73���ͣ�50��67�����뺯������ʽ��
��![]() ���
��� 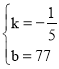
�� ![]() ��
��
��![]() ������ʽ��
������ʽ��
�ɵã�![]()
���Ըñ仯���ɲ���һ�κ���.
���ټ���仯����Ϊ����������![]() ��
��
����20��73�����뺯������ʽ����![]() ��
��
��![]() ��
��
��![]() ������ʽ��
������ʽ��
�ɵ�![]()
���Ըñ仯���ɲ��Ƿ���������.
�ۼ���仯����Ϊ���κ���![]()
����20��73������50��67���ͣ�70��83�����뺯������ʽ��
��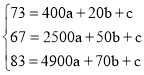 ���
��� 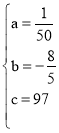
��![]()
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��ö��κ����������е㣬
�ʸñ仯����Ϊ���κ���������ʽΪ��![]() .
.
��2���ɣ�1����֪![]() ��
��
���Ե�![]() ʱ��
ʱ��![]() ֵ��С������СֵΪ65.
ֵ��С������СֵΪ65.
������ת�Ƕ�Ϊ40��ʱ���տ�һ��ˮ����ȼ�������٣�����Ϊ65��.
��3����ü�ͥ����ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ��![]() �����ף�
�����ף�
���ݽ�Լǰ��ı�����ȼ������������Լ�ı�����ȣ�
��![]() ��
��
���![]() �������ף���
�������ף���
���ü�ͥ����ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ��![]() ������.
������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
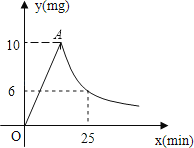
����Ŀ���Ϸ���ʮ����ΪԤ���^�����������Խ��ҽ��С�ҩ����������֪ҩ����ȼ���ͷŹ����У����ڿ�����ÿ������ҩ��![]() �����ˣ���ȼ��ʱ��
�����ˣ���ȼ��ʱ��![]() �����ӣ�֮��Ĺ�ϵ��ͼ��ʾ����ͼ���߶�
�����ӣ�֮��Ĺ�ϵ��ͼ��ʾ����ͼ���߶�![]() ��˫������
��˫������![]() �㼰���Ҳ�IJ��֣�������ͼ����ʾ��Ϣ������������⣺
�㼰���Ҳ�IJ��֣�������ͼ����ʾ��Ϣ������������⣺
��1��д����ҩ���ͷſ�ʼ��![]() ��
��![]() ֮��ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
֮��ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
��2���ݲⶨ��ֻ�е�������ÿ�����ĺ�ҩ��������![]() ����ʱ����Ԥ���������ã������ٳ�������
����ʱ����Ԥ���������ã������ٳ�������![]() �������ϣ�������ȫɱ�����ֲ�����������������Ƿף�
�������ϣ�������ȫɱ�����ֲ�����������������Ƿף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=![]() �����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ
�����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ![]() ����EB��ED����S��APD+S��APB=1+
����EB��ED����S��APD+S��APB=1+![]() ����S������ABCD=4+
����S������ABCD=4+![]() ��������ȷ���۵�����ǣ� ��
��������ȷ���۵�����ǣ� ��

A.�٢ۢ� B���٢ڢ� C���ۢܢ� D���٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,![]() ��
��![]() �ı�
�ı�![]() ���е�,��
���е�,��![]() �ӳ����ϵĵ�
�ӳ����ϵĵ�![]() ��
��![]() �Ĵ���
�Ĵ���![]() ,
,![]() ����,
����,![]() ��
��![]() ���ӳ����ཻ�ڵ�
���ӳ����ཻ�ڵ�![]() ,��
,��![]() ��
��![]() ��,
��,![]() ,
,![]() ��
��![]() ��
��
��1��֤����![]() ��
��
��2��֤������![]() ��
��![]() �����Բ��Բ�ģ�
�����Բ��Բ�ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���㣨-2��-3���͵㣨1��6��
���㣨-2��-3���͵㣨1��6��
��1������������Ľ���ʽ��
��2����![]() ��ʲô��Χ��ʱ������ֵ
��ʲô��Χ��ʱ������ֵ![]() ��
��![]() �����������
�����������
��3�������������ͼ����![]() ��Ľ�������.
��Ľ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��һ����������γ̸ĸ�����������ʽ���Ҫ���ѧУ�γ���ϵ��ijѧУ����������A�鷨��B�Ķ���C����D��������У��ѡ�γ̹�ѧ��ѡ��ÿ�ſγ̱�ѡ���Ļ�����ȣ�
��1��ѧ��С��ƻ�ѡ�����ſγ̣���д�����п��ܵ�ѡ����
��2����ѧ��С����С�ո��ƻ�����һ�ſγ̣�����������ǡ��ѡ��ͬһ�ſγ̵ĸ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+4x+c��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��y=-x+5������B��C��
��1���������ߵı���ʽ��
��2����D��1��0������PΪ�Գ�����һ���㣬����BP��CP��
������CPB=90�������P�����ꣻ
�ڵ�QΪ��������һ���㣬����C��D��P��QΪ������ı�����ƽ���ı��Σ���P�����꣮
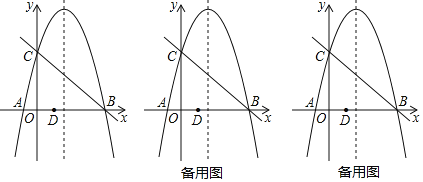
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ������������Ŀڴ��У��ֱ��д�С��������ȫ��ͬ��С�����мڴ��е�С���Ϸֱ��������1��2��3��4���ҿڴ��е�С���Ϸֱ��������2��3��4���ȴӼ״�����������һ��С��������Ϊm���ٴ��Ҵ�������һ��С��������Ϊn��
��1�������б�����״ͼ�ķ�����ʾ�����У�m��n�����ܵĽ����
��2����m��n���Ƿ���x2��5x+6��0�Ľ�ʱ����С����ʤ����m��n�����Ƿ���x2��5x+6��0�Ľ�ʱ����С����ʤ������������˭��ʤ�ĸ��ʴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019���й����������ղ�����(���¼����������)��4��29����10��7���ڱ������������У�����Ϊ�����ҵ������������������4��������ɫ��Ȥ��·�ߣ��ֱ��ǣ�![]() ����������������
����������������![]() �������Ҽң���������
�������Ҽң���������![]() ������С����֮������
������С����֮������![]() �������ٳ���֮�������������ŷ����ƻ����ȥ���ᣬ���Ǹ�������4����·������ѡ��һ����·������ÿ����·��ѡ��Ŀ�������ͬ��
�������ٳ���֮�������������ŷ����ƻ����ȥ���ᣬ���Ǹ�������4����·������ѡ��һ����·������ÿ����·��ѡ��Ŀ�������ͬ��
(1)����ѡ����·![]() ������С����֮�����ĸ����Ƕ��٣�
������С����֮�����ĸ����Ƕ��٣�
(2)�û���״ͼ���б��ķ��������������ŷ�ǡ��ѡ��ͬһ��·�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com