
【题目】已知,![]() 与
与![]() 两角的角平分线交于点
两角的角平分线交于点![]() ,
,![]() 是射线
是射线![]() 上一个动点,过点
上一个动点,过点![]() 的直线分别交射线
的直线分别交射线![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
(1)如图1,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,若![]() ,请探索
,请探索![]() 与
与![]() 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;
(3)在点![]() 运动的过程中,请直接写出
运动的过程中,请直接写出![]() ,
,![]() 与
与![]() 这三个角之间满足的数量关系:_________________________________.
这三个角之间满足的数量关系:_________________________________.


【答案】(1)![]() ;(2)
;(2)![]() ,证明详见解析;(3)
,证明详见解析;(3)![]() 或
或![]()
【解析】
(1)根据角平分线的性质结合三角形外角的性质即可求解;
(2)设![]() ,
,![]() ,根据角平分线的性质结合四边形内角和定理即可求解;
,根据角平分线的性质结合四边形内角和定理即可求解;
(3)分点P在线段BD上和点P在线段BD的延长线上两种情况讨论即可求解.
(1)∵PA、PB是∠BAM、∠ABN的角平分线,
∴∠BAP=∠PAE=![]() ∠BAM=
∠BAM=![]() ,
,
∠ABP=∠PBE=![]() ∠ABN=
∠ABN=![]() ,
,
∴∠BPC=∠BAP+∠ABP=![]() ;
;
(2)![]() ,理由如下:
,理由如下:
∵PA、PB是∠BAM、∠ABN的角平分线,
∴设![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)∵PA、PB是∠BAM、∠ABN的角平分线,
∴设![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
如图,当点P在线段BD上时,

![]() ,
,
∴![]() ;
;
如图,当点P在线段BD的延长线上时,
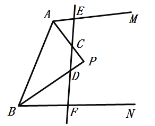
![]() ,即
,即![]() ,
,
∴![]() ,
,
即![]() ;
;


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=_______,△APE的面积等于8.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RT△ABC中,∠ACB=90°,∠B=35°,CD⊥AB,垂足为点D,

(1)求∠ACD的度数;
(2)找出图中相等的角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y=![]() ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“品中华诗词,寻文化自信”.某校组织全校1000名学生举办了第二届“中华诗词大赛”的初赛,从中抽取部分学生的成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩 | 人数 | 百分比 |
|
| 8 | 20% |
|
| 16 |
|
|
|
| 30% |
|
| 4 | 10% |
频数分布直方图

请观察图表,解答下列问题:
(1)表中![]() __________,
__________,![]() __________;
__________;
(2)补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,那么请你估计该校进入决赛的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
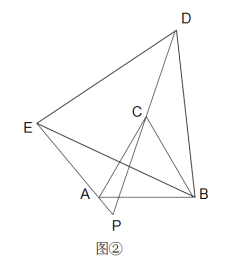
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=a.
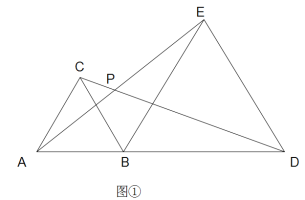
(1)当a=60°, 如图①则,∠DPE的度数______________
(2)若△BDE绕点B旋转一定角度,如图②所示,求∠DPE(用a表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进一批跳绳,若购进![]() 种跳绳
种跳绳![]() 根和
根和![]() 种跳绳
种跳绳![]() 根,则共需
根,则共需![]() 元;若购进
元;若购进![]() 种跳绳
种跳绳![]() 根和
根和![]() 种跳绳
种跳绳![]() 根,则共需
根,则共需![]() 元.
元.
(1)求![]() 、
、![]() 两种跳绳的单价各是多少?
两种跳绳的单价各是多少?
(2)若该商店准备购进这两种跳绳共![]() 根,且
根,且![]() 种跳绳的数量不少于跳绳总数量的
种跳绳的数量不少于跳绳总数量的![]() .若每根
.若每根![]() 种、
种、![]() 种跳绳的售价分别为
种跳绳的售价分别为![]() 元、
元、![]() 元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com