【题目】某商店欲购进一批跳绳，若购进
种跳绳
根和
种跳绳
根，则共需
元；若购进种跳绳
根和种跳绳
根，则共需
元．
（1）求、两种跳绳的单价各是多少？
（2）若该商店准备购进这两种跳绳共
根，且种跳绳的数量不少于跳绳总数量的
．若每根种、种跳绳的售价分别为
元、
元，问：该商店应如何进货才可获取最大利润，并求出最大利润．
【答案】（1）A种跳绳的单价为22元，B种跳绳的单价为25元.
（2）该商店应购进A种跳绳56根，B种跳绳84根，可获取最大利润，最大利润是952元.
【解析】
（1）设A种跳绳的单价为x元，B种跳绳的单价为y元. 构建方程组即可解决问题；
（2）设购进A种跳绳a根，则B种跳绳(140-a)根，该商店的利润为w元，根据题意得出一次函数，再利用一次函数的性质即可解决问题.
解：（1）设A种跳绳的单价为x元，B种跳绳的单价为y元. 由题意，得
解得 
答：A种跳绳的单价为22元，B种跳绳的单价为25元.
（2）设购进A种跳绳a根，则B种跳绳(140-a)根，该商店的利润为w元，根据题意得
w=(27-22)a+(33-25)(140-a)=-3a+1120
∵-3＜0
∴a取最小值时，w取最大值
∵a≥140×
即a≥56，且a为整数
∴当a=56时，w最大=-3×56+1120=952
此时，140-56=84（根）
答：该商店应购进A种跳绳56根，B种跳绳84根，可获取最大利润，最大利润是952元.
故答案为（1）A种跳绳的单价为22元，B种跳绳的单价为25元.
（2）该商店应购进A种跳绳56根，B种跳绳84根，可获取最大利润，最大利润是952元.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知，
与
两角的角平分线交于点
，
是射线
上一个动点，过点的直线分别交射线
，
，
于点
，
，
．
（1）如图1，若
，
，
，求
的度数；
（2）如图2，若
，请探索
与
的数量关系，并证明你的结论；
（3）在点运动的过程中，请直接写出，与这三个角之间满足的数量关系：_________________________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探究：
（1）如图1，在△ABC与△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°,连结BD、CE．请写出图1中所有全等的三角形： （不添加字母）．
（2）如图2，已知△ABC，AB＝AC，∠BAC＝90°，
是过A点的直线，CN⊥，BM⊥，垂足为N、M．求证：△ABM≌△CAN．
解决问题：
（3）如图3，已知△ABC,AB＝AC,∠BAC＝90°,D在边BC上,DA＝DE,∠ADE ＝90°．
求证：AC⊥CE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠A＝20°，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，依此类推，∠ABD4与∠ACD4的角平分线交于点D5，则∠BD5C的度数是_____．
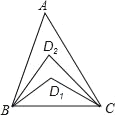
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC，此时点D落在AB边上，斜边DE交AC于点F，则n的大小和图中阴影部分的面积分别为（ ）
A. 30，2 B. 60，2 C. 60，
D. 60，
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一次800米的长跑比赛中，甲、乙两人所跑的路程
（米）与各自所用时间
（秒）之间的函数图象分别为线段
和折线
（如图所示），请根据图象，回答下列问题.
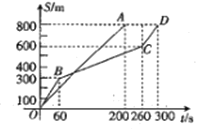
（1）在起跑后60秒时，乙在甲的前面还是后面？
（2）在起跑后多少秒时，两人相遇？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB∥CD，∠E=90°，那么∠B+∠D等于多少度？为什么？
解：过点E作EF∥AB，
得∠B+∠BEF=180°（________________________）,
因为AB∥CD（已知），
EF∥AB（所作），
所以EF//CD（________________________）.
得________________________（两直线平行，同旁内角互补），
所以∠B+∠BEF+∠DEF+∠D=________°（__________）.
即∠B+∠BED+∠D=___________°.
因为∠BED=90°（已知），
所以∠B+∠D=___________°（等式性质）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
