
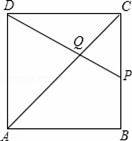
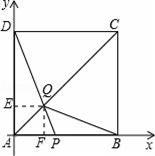
��ͼ���ڱ߳�Ϊ4��������ABCD�У���P��AB�ϴ�A��B�˶�������DP��AC�ڵ�Q��
��1����֤�������۵�P�˶���AB�Ϻδ�ʱ�����С�ADQ�ա�ABQ��
��2������P��AB���˶���ʲôλ��ʱ����ADQ�������������ABCD�����
 ��
��
��3������P�ӵ�A�˶�����B���ټ�����BC���˶�����C���������˶������У�����P�˶���ʲôλ��ʱ����ADQǡΪ���������Σ�


�����㡿�����ε����ʣ������ε������ȫ�������ε��ж������������ε��ж������������ε��ж������ʣ�
����������1������SAS��á�ADQ�ա�ABQ��
��2������Q��QE��AD��E��QF��AB��F����QE=QF������ADQ�������������ABCD�����
 ������S��ADQ=
������S��ADQ=
 AD•QE=
AD•QE=
 S������ABCD�����OE��ֵ�������á�DEQ�ס�DAP��
S������ABCD�����OE��ֵ�������á�DEQ�ס�DAP��
 ���APֵ��
���APֵ��
��3����P�˶�ʱ����ADQǡΪ���������ε���������֣���QD=QA��DA=DQ��AQ=AD���������ε�����֪���ٵ���P�˶������B�غ�ʱ��QD=QA����ʱ��ADQ�ǵ��������Σ��ڵ���P���C�غ�ʱ����Q���CҲ�غϣ���ʱDA=DQ����ADQ�ǵ��������Σ��۵�AD=AQ=4ʱ����CP=CQ��CP=AC��AD���������εĶԽ��ߵ����ʵõ�CP��ֵ��
����𡿣�1��֤������������ABCD�У�
���۵�P�˶���AB�Ϻδ�ʱ������
AD=AB����DAQ=��BAQ��AQ=AQ��
���ADQ�ա�ABQ��
��2���ⷨһ����ADQ�����ǡ����������ABCD�����
 ʱ��
ʱ��
����Q��QE��AD��E��QF��AB��F����QE=QF��
���ڱ߳�Ϊ4��������ABCD�У�
��S������ABCD=16��
��
 AD��QE=
AD��QE=
 S������ABCD=
S������ABCD=
 ��16=
��16=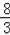
 ��
��
��QE=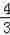
 ��
��
��EQ��AP��
���DEQ�ס�DAP��
��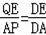
 ����
����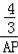
 =
=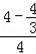
 ��
��
���AP=2��
��AP=2ʱ����ADQ�������������ABCD�����
 ��
��
�ⷨ������AΪԭ�㽨����ͼ��ʾ��ֱ������ϵ������Q��QE��y���ڵ�E��QF��x���ڵ�F��

 AD��QE=
AD��QE=
 S������ABCD=
S������ABCD=
 ��16=
��16=
 ��
��
��QE=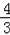
 ��
��
�ߵ�Q�������ζԽ���AC�ϣ�
��Q���������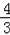
 ��
��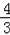
 ����
����
�����D��0��4����Q��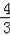
 ��
��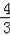
 ������ĺ�����ϵʽΪ��y=��2x+4��
������ĺ�����ϵʽΪ��y=��2x+4��
��y=0ʱ��x=2��
��P���������2��0����
��AP=2ʱ��������P�˶���AB�е�λ��ʱ����ADQ�������������ABCD�����
 ��
��
��3���⣺����ADQ�ǵ��������Σ�����QD=QA��DA=DQ��AQ=AD��
�ٵ�AD=DQʱ�����DQA=��DAQ=45��
���ADQ=90�㣬PΪC�㣬
�ڵ�AQ=DQʱ�����DAQ=��ADQ=45�㣬
���AQD=90�㣬PΪB��
��AD=AQ��P��BC�ϣ���
��CQ=AC��AQ=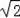
 BC��BC=��
BC��BC=��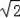
 ��1��BC
��1��BC
��AD��BC
��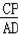
 =
=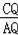
 �����ɵ�
�����ɵ�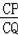
 =
=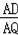
 =1��
=1��
��CP=CQ=��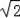
 ��1��BC=4��
��1��BC=4��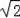
 ��1��
��1��
���ϣ�P��B�㣬C�㣬����CP=4��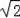
 ��1��������ADQ�ǵ��������Σ�
��1��������ADQ�ǵ��������Σ�


��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ����һ������ABCDֽƬ����ȥ������ȫ��ͬ�ľ��κ�ʣ�����Ӱ����ֽƬ�����СΪ24����AB=8�������ľ��εij�Ϊ��������������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����Rt��ABC�У���ACB=90�㣬AC=5cm��BC=12cm������ABC�Ƶ�B˳ʱ����ת60�㣬�õ���BDE������DC��AB�ڵ�F�����ACF���BDF���ܳ�֮��Ϊ������������cm��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ijС����30���������˾�����������Ƴ�����Ƶ���ֲ�ֱ��ͼ��������1200��1240Ԫ��Ƶ���ǣ�������


A��12 B��13 C��14 D��15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪�߶�AB��BC����ABC=90�㣬��������ABCD��
��1��С��ͬѧ����ͼ�ۼ���ͼ������д������������
��2�������������һ�ֳ߹���ͼ�ķ�����������ͼ�Σ������ۼ�������д������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ��DEΪ��ABC����λ�ߣ���F��DE�ϣ��ҡ�AFB=90�㣬��AB=5��BC=8����EF�ij�Ϊ��������������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ, ��ƽ��ֱ������ϵ��,��A��B�ֱ���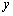 ��������,
��������,  ����������������,
����������������,  ��
�� ����AO��BOΪ�ڱ߹������AOBC��������
����AO��BOΪ�ڱ߹������AOBC�������� ��
��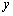 ���ڵ�D��PΪ���㣬PM��
���ڵ�D��PΪ���㣬PM�� ���ڵ�M��
���ڵ�M��
��1����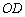 ��
�� �ij�(������ú�
�ij�(������ú� �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
��2���� ʱ,��������ߵı���ʽ��
ʱ,��������ߵı���ʽ��
��3���ڵ� �������˶������У�
�������˶������У�
�������� �ǵ���������,�������������������
�ǵ���������,������������������� ��ֵ��
��ֵ��
 �ڵ���A����ֱ��DP�ĶԳƵ�
�ڵ���A����ֱ��DP�ĶԳƵ� ǡ������������
ǡ������������ ��ͼ����ʱ����ֱ��д��
��ͼ����ʱ����ֱ��д�� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com