
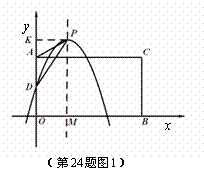
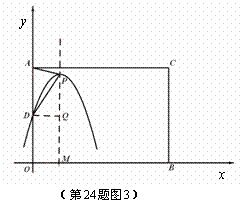
如图, 在平面直角坐标系中,点A,B分别是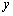 轴正半轴,
轴正半轴,  轴正半轴上两动点,
轴正半轴上两动点,  ,
, ,以AO,BO为邻边构造矩形AOBC,抛物线
,以AO,BO为邻边构造矩形AOBC,抛物线 交
交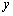 轴于点D,P为顶点,PM⊥
轴于点D,P为顶点,PM⊥ 轴于点M.
轴于点M.
(1)求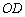 ,
, 的长(结果均用含
的长(结果均用含 的代数式表示).
的代数式表示).
(2)当 时,求该抛物线的表达式.
时,求该抛物线的表达式.
(3)在点 在整个运动过程中.
在整个运动过程中.
①若存在 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的 的值.
的值.
 ②当点A关于直线DP的对称点
②当点A关于直线DP的对称点 恰好落在抛物线
恰好落在抛物线 的图象上时,请直接写出
的图象上时,请直接写出 的值.
的值.
解:(1)把x=0,代入 ,得
,得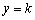 .∴
.∴ .
.
∵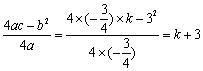 ,∴
,∴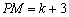 . (3分)
. (3分)
(2)∵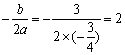 ,∴
,∴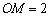 ,
,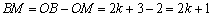 .
.
又∵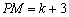 ,
, ,∴
,∴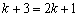 ,解得
,解得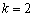 .
.
∴该抛物线的表达式为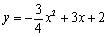 . (3分)
. (3分)
(3)①
Ⅰ)当点P在矩形AOBC外部时
如图1,过P作PK⊥OA于点K,当AD=AP时,
∵AD=AO-DO=2k-k=k,
∴AD=AP =k,KA=KO-AO=PM-AO=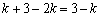
 KP=OM=2,在Rt△KAP中,
KP=OM=2,在Rt△KAP中,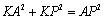
∴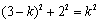 ,解得
,解得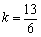 .
.
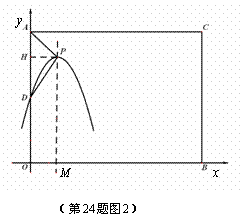
Ⅱ)当点P在矩形AOBC内部时
当PD=AP时,如图2,过P作PH⊥OA于H,
AD=k,HD=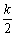 ,
,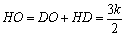
又∵HO=PM=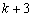 ,
,
∴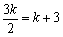 ,解得
,解得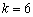 .
.
当DP=DA时,如图3,过D作PQ⊥PM于Q,
PQ=PM-QM=PM-OD=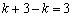
DQ=OM=2,DP=DA=k,
在Rt△DQP中,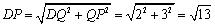 .
.
∴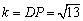 . (6分)
. (6分)
② .
.
 | |||
 | |||


科目:初中数学 来源: 题型:
如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.
(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的
 ;
;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.


查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的口袋里装有1个红球,2个白球和n个黄球,这些球除颜色外其余都相同.若从该口袋中任意摸出1个球,摸到白球的可能性大于黄球的可能性,则n等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知点A(3,4),B( 3,0).
3,0).
(1)只用直尺(没有刻度)和圆规按下列要求作图.
(要求:保留作图痕迹,不必写出作法)
Ⅰ)AC⊥y轴,垂足为C;
Ⅱ)连结AO,AB,设边AB,CO交点E.
(2)在(1)作出图形后,直接判断△AOE与△BOE的面积大小关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com