
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为 cm.


42 cm.
【考点】旋转的性质.
【分析】根据将△ABC绕点B顺时针旋转60°,得到△BDE,可得△ABC≌△BDE,∠CBD=60°,BD=BC=12cm,从而得到△BCD为等边三角形,得到CD=BC=CD=12cm,在Rt△ACB中,利用勾股定理得到AB=13,所以△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD,即可解答.
【解答】解:∵将△ABC绕点B顺时针旋转60°,得到△BDE,
∴△ABC≌△BDE,∠CBD=60°,
∴BD=BC=12cm,
∴△BCD为等边三角形,
∴CD=BC=CD=12cm,
在Rt△ACB中,AB=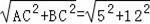
 =13,
=13,
△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=5+13+12+12=42(cm),
故答案为:42.


科目:初中数学 来源: 题型:
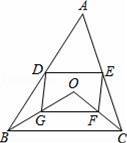
.D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.
(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的
 ;
;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.


查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的口袋里装有1个红球,2个白球和n个黄球,这些球除颜色外其余都相同.若从该口袋中任意摸出1个球,摸到白球的可能性大于黄球的可能性,则n等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com