
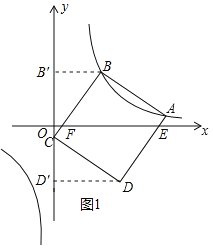
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图象经过正方形ABCD的顶点A和B,点C、D的坐标分别是(0,﹣1)和(4,﹣3),边AD,BC分别交x轴于点E、F.
的图象经过正方形ABCD的顶点A和B,点C、D的坐标分别是(0,﹣1)和(4,﹣3),边AD,BC分别交x轴于点E、F.

(1)填空:正方形的边长为 ;
(2)求反比例函数y=![]() 的解析式;
的解析式;
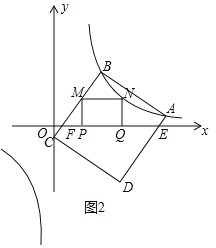
(3)若点M是直线BC上一动点,作MN∥x轴,交反比例函数y=![]() 的图象于点N,过点M,N分别向x轴作垂线,垂足分别为P、Q,得到矩形MPQN,设点M的横坐标为a.
的图象于点N,过点M,N分别向x轴作垂线,垂足分别为P、Q,得到矩形MPQN,设点M的横坐标为a.
①填空:点N的坐标为 ;(用含a的代数式表示)
②填空:若矩形MPQN的面积为6,则点M的横坐标为 .
【答案】(1)2![]() ;(2)
;(2)![]() (3)0,
(3)0,![]() 或
或![]()
【解析】
(1)由点C,D的坐标,利用两点间的距离公式可求出CD的长,此问得解;
(2)过点B作BB′⊥y轴于点B′,过点D作DD′⊥y轴于点D′,则△B′BC≌△D′CD(AAS),利用全等三角形的性质可求出BB′,CB′,OB′的长度,进而可得出点B的坐标,由点B的坐标,利用待定系数法即可求出反比例函数解析式;
(3)①由点B,C的坐标,利用待定系数法可求出直线BC的解析式,由点M的横坐标为a,利用一次函数图象上点的坐标特征及反比例函数图象上点的坐标特征,可得出点M,N的坐标;
②由点M,N的坐标,可得出MN,MP的长,由矩形的面积公式结合矩形MPQN的面积为6,可得出关于a的方程,解之经检验后即可得出结论.
(1)∵点C的坐标为(0,﹣1),点D的坐标为(4,﹣3),
∴CD=![]() ,
,
故答案为:2![]() ;
;
(2)过点B作BB′⊥y轴于点B′,过点D作DD′⊥y轴于点D′,如图1所示,
∵四边形ABCD为正方形,
∴∠BCD=90°,BC=CD.
∵∠B′BC+∠B′CB=90°,∠B′CB+∠D′CD=90°,
∴∠B′BC=∠D′CD,
在△B′BC和△D′CD中,
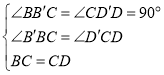 ,
,
∴△B′BC≌△D′CD(AAS),
∴BB′=CD′=2,CB′=DD′=4,
∴OB′=CB′﹣OC=3,
∴点B的坐标为(2,3),
将B(2,3)代入y=![]() ,得:3=
,得:3=![]() ,
,
∴k=6,
∴反比例函数的解析式为y=![]() ;
;
(3)①设直线BC的解析式为y=mx+n(m≠0),
将B(2,3),C(0,﹣1)代入y=mx+n,得:
![]() ,解得:
,解得:![]() ,
,
∴直线BC的解析式为y=2x﹣1,
∵点M的横坐标为a,
∴点M的坐标为(a,2a﹣1),
∵MN∥x轴,且点N反比例函数y=![]() 的图象上,
的图象上,
∴点N的坐标为(![]() ,2a﹣1),
,2a﹣1),
故答案为:(![]() ,2a﹣1);
,2a﹣1);
②∵点M的坐标为(a,2a﹣1),点N的坐标为(![]() ,2a﹣1),
,2a﹣1),
∴MN=|a﹣![]() |,MP=|2a﹣1|,
|,MP=|2a﹣1|,
∵矩形MPQN的面积为6,
∴|a﹣![]() ||2a﹣1|=6,即2a2﹣a=0或2a2﹣a﹣12=0,
||2a﹣1|=6,即2a2﹣a=0或2a2﹣a﹣12=0,
解得:a1=0,a2=![]() ,a3=
,a3=![]() ,a4=
,a4=![]() ,
,
经检验,a1=0,a3=![]() ,a4=
,a4=![]() 是原方程的解,且符合题意,a2=
是原方程的解,且符合题意,a2=![]() 是增根,舍去,
是增根,舍去,
故答案为:0,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若cosC=![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
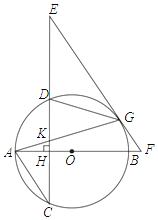
查看答案和解析>>
科目:初中数学 来源: 题型:
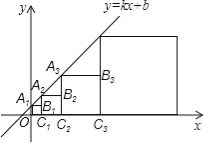
【题目】在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() 的顶点A在格点上,B是小正方形边的中点,
的顶点A在格点上,B是小正方形边的中点,![]() ,
,![]() ,经过点A,B的圆的圆心在边AC上.
,经过点A,B的圆的圆心在边AC上.
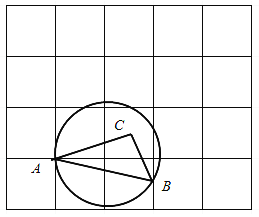
(Ⅰ)线段AB的长等于_______________;
(Ⅱ)请用无刻度的直尺,在如图所示的网格中,画出一个点P,使其满足![]() ,并简要说明点P的位置是如何找到的(不要求证明)_____.
,并简要说明点P的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
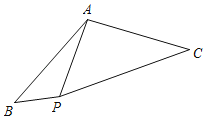
【题目】如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC的内部有一点P,PA=8,PB=4,PC=4![]() ,则线段AB的长为_____.
,则线段AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)
甲:5、6、7、9、8
乙:8、4、8、6、9
(1)分别计算这两组数据的平均数和方差;
(2)根据测试成绩,你认为选派哪一名选手参赛更好些?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 是常数),
是常数),![]() ,顶点坐标为
,顶点坐标为![]() .给出下列结论:①若点
.给出下列结论:①若点![]() 与点
与点![]() 在该抛物线上,当
在该抛物线上,当![]() 时,则
时,则![]() ;②关于
;②关于![]() 的一元二次方程
的一元二次方程![]() 无实数解,那么( )
无实数解,那么( )
A.①正确,②正确B.①正确,②错误C.①错误,②正确D.①错误,②错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“心灵信箱”的设立,为师、生之间的沟通开设了一个书面交流的渠道.为了解九年级学生对“心灵信箱”开通两年来的使用情况,某课题组对该校九年级全体学生进行了一次问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
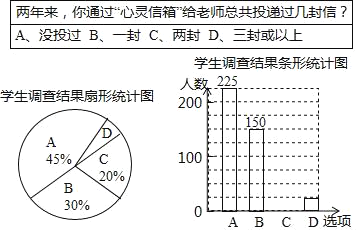
根据图表,解答以下问题:
(1)该校九年级学生共有 人;
(2)学生调查结果扇形统计图中,扇形D的圆心角度数是 ;
(3)请你补充条形统计图;
(4)根据调查结果可以推断:两年来,该校九年级学生通过“心灵信箱”投递出的信件总数至少有 封.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com