
【题目】已知:抛物线![]()
![]() 的顶点为A,与x轴的交点为B,C(点B在点C的左侧).
的顶点为A,与x轴的交点为B,C(点B在点C的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请写出a,b满足的关系式;若不能,说明理由.
【答案】(1)抛物线对称轴方程:![]() .(2)
.(2)![]() ,
,![]() 或
或![]() ,
,![]() .(3)
.(3)![]() .
.
【解析】
(1)根据y=a(x-2)2+b直接得出答案;
(2)根据直线x=2与x轴交于点E,则E(2,0),以及抛物线经过原点,得出B(0,0),C(4,0),进而求出AE=BE=EC,当抛物线的顶点为A(2,-2)时,以及当抛物线的顶点为A′(2,2)时求出即可;
(3)根据B、C关于点E中心对称,当A,D也关于点E对称,且BE=AE时,四边形ABDC是正方形,即可求出.
(1)抛物线对称轴方程:直线x=2.
(2)如图,
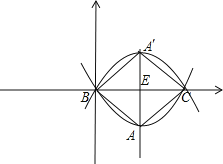
设直线x=2与x轴交于点E,则E(2,0).
∵抛物线经过原点,
∴B(0,0),C(4,0).(3分)
∵△ABC为直角三角形,根据抛物线的对称性可知AB=AC,
∴AE=BE=EC,
∴A(2,-2)或(2,2).
当抛物线的顶点为A(2,-2)时,y=a(x-2)2-2,
把(0,0)代入,得:a=![]() ,
,
此时,b=-2.
当抛物线的顶点为A′(2,2)时,y=a(x-2)2+2,
把(0,0)代入,得:a=![]() ,此时,b=2.
,此时,b=2.
∴a=![]() ,b=-2或a=
,b=-2或a=![]() ,b=2.
,b=2.
(3)依题意,B、C关于点E中心对称,当A,D也关于点E对称,且BE=AE时,四边形ABDC是正方形.
∵A(2,b),
∴AE=|b|,
∴B(2-|b|,0),
把B(2-|b|,0)代入y=a(x-2)2+b,得ab2+b=0,
∵b≠0,
∴abb+b=0,
∴b=-ab2,即![]() =-1,-ab=1,
=-1,-ab=1,
∴ab=-1.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2)点M是边BC上的一个动点(不与B、C重合),反比例函数![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
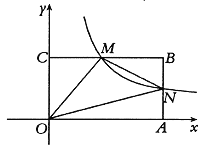
(1)当点M是边BC的中点时,求反比例函数的表达式;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
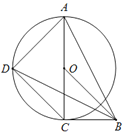
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径作⊙O,D为⊙O上一点,连接AD、BD、CD、OB,且BD=AB.
(1)求证:OB//CD;
(2)若D为弧AC的中点,求tan∠BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() (
(![]() )经过点
)经过点![]() 、B.
、B.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() (
(![]() )的函数值随
)的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当行驶中的汽车撞到物体时,汽车的损坏程度通常用“撞击影响”来衡量.汽车的撞击影响I可以用汽车行驶速度v(km/min)来表示,下表是某种型号汽车的行驶速度与撞击影响的试验数据:
v(km/min) | 0 | 1 | 2 | 3 | 4 |
I | 0 | 2 | 8 | 18 | 32 |
(1)请根据上表中的数据,在直角坐标系中描出坐标(v,I)所对应的点,并用光滑曲线将各点连接起来;

(2)填写下表,并根据表中数据的呈现规律,猜想用v表示I的二次函数表达式;
v(km/min) | 1 | 2 | 3 | 4 |
|
|
|
|
|
(3)当汽车的速度分别是1.5 km/min,2.5 km/min,4.5 km/min时,利用你得到的撞击影响公式,计算撞击影响分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E是BC边上一点,连接AE.
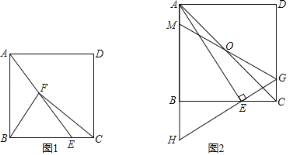
(1)如图1,点F为AE的中点,连接CF.已知tan∠FBE=![]() ,BF=5,求CF的长;
,BF=5,求CF的长;
(2)如图2,过点E作AE的垂线交CD于点G,交AB的延长线于点H,点O为对角线AC的中点,连接GO并延长交AB于点M,求证:AM+BH=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com