
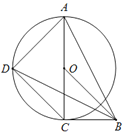
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径作⊙O,D为⊙O上一点,连接AD、BD、CD、OB,且BD=AB.
(1)求证:OB//CD;
(2)若D为弧AC的中点,求tan∠BDC.
【答案】(1)证明见解析;(2)tan∠BDC=![]() .
.
【解析】
(1)先利用边边边定理判定![]() ,再由等腰三角形的性质、直径所对的圆周角是直角得到
,再由等腰三角形的性质、直径所对的圆周角是直角得到![]() 、
、![]() ,最后根据同位角相等推出两直线平行;
,最后根据同位角相等推出两直线平行;
(2)由D为弧AC的中点,可得![]() 、
、![]() 为等腰直角三角形,在
为等腰直角三角形,在![]() 中利用锐角三角函数求得
中利用锐角三角函数求得![]() ,即可得
,即可得![]() .
.
解:(1)证明:连结OD,延长OE交AD于点E,如图:
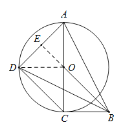
∵AO=OD,AB=BD,OB=OB
∴△ABO≌△DBO
∴∠ABO=∠DBO
∴∠AEB=90°
∵AC是⊙O的直径
∴∠ADC=90°
∴∠AEB=∠ADC
∴OB//CD
(2)∵D为弧AC的中点
∴∠DOC=∠DOA=90°,∠DCO=∠DAO=45°,AD=CD
∵∠ACB=90°
∴OD//BC
∵OB//CD
∴四边形ODCB平行四边形
∴OB=CD,∠BDC=∠DBE
∴设OE=x,则DE=x,OD=![]() x,CD=2x
x,CD=2x
∴BE=x+2x=3x
∴tan∠BDC=tan∠DBE=![]() .
.
故答案是:(1)证明见解析;(2)![]()


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
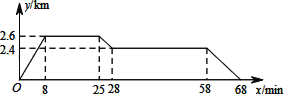
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为适应新中考英语听说机考,九年级甲、乙两位同学使用某手机软件进行英语听说练习并记录了40次的练习成绩.甲、乙两位同学的练习成绩统计结果如图所示:

下列说法正确的是( )
A. 甲同学的练习成绩的中位数是38分
B. 乙同学的练习成绩的众数是15分
C. 甲同学的练习成绩比乙同学的练习成绩更稳定
D. 甲同学的练习总成绩比乙同学的练习总成绩低
查看答案和解析>>
科目:初中数学 来源: 题型:
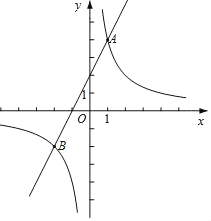
【题目】如图,在平面直角坐标系xOy中,直线y=2x+2与函数y=![]() (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求k,m的值;
(2)已知点P(a,0),过点P作平行于y轴的直线,交直线y=2x+2于点M,交函数y=![]() (k≠)的图象于点N.
(k≠)的图象于点N.
①当a=2时,求线段MN的长;
②若PM>PN,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
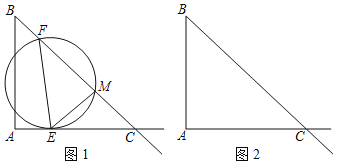
【题目】如图,Rt△ABC中,AB=6,AC=8.动点E,F同时分别从点A,B出发,分别沿着射线AC和射线BC的方向均以每秒1个单位的速度运动,连接EF,以EF为直径作⊙O交射线BC于点M,连接EM,设运动的时间为t(t>0).
(1)当点E在线段AC上时,用关于t的代数式表示CE= ,CM= .(直接写出结果)
(2)在整个运动过程中,当t为何值时,以点E、F、M为顶点的三角形与以点A、B、C为顶点的三角形相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]()
![]() 的顶点为A,与x轴的交点为B,C(点B在点C的左侧).
的顶点为A,与x轴的交点为B,C(点B在点C的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请写出a,b满足的关系式;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程![]() ,
,![]() ,其中
,其中![]() ,下列四个结论中,错误的是( )
,下列四个结论中,错误的是( )
A. 如果方程![]() 有两个不相等的实数根,那么方程
有两个不相等的实数根,那么方程![]() 也有两个不相等的实数根
也有两个不相等的实数根
B. ![]() 时,方程
时,方程![]() 和方程
和方程![]() 有一个相同的根,那么这个根必是
有一个相同的根,那么这个根必是![]()
C. 如果![]() 是方程
是方程![]() 的一个根,那么
的一个根,那么![]() 是方程
是方程![]() 的一个根
的一个根
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com