
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)当t为何值时,△PQF为等腰三角形?试说明理由.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某公司销售甲、乙两种运动鞋,2018年这两种鞋共卖出11000双。2019年甲种运动鞋卖出的数量比2018年增加6%,乙种运动鞋卖出的数量比2018年减少5%,且这两种鞋的总销量增加了2%.
(1)求2018年甲、乙两种运动鞋各卖了多少双?
(2)某制鞋厂组织工人生产甲、乙两种运动鞋。原计划安排 ![]() 的工人生产甲种运动鞋,现抽调其中的16人去生产乙种运动鞋,已知每位工人一天可生产甲种运动鞋6双或乙种运动鞋4双,若调配后制成的两种运动鞋数量相等,求该鞋厂工人的人数。
的工人生产甲种运动鞋,现抽调其中的16人去生产乙种运动鞋,已知每位工人一天可生产甲种运动鞋6双或乙种运动鞋4双,若调配后制成的两种运动鞋数量相等,求该鞋厂工人的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是正方形网格中的三个格点.
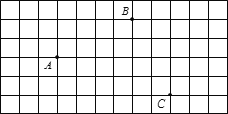
(1)①画射线AC;
②画线段BC;
③过点B画AC的平行线BD;
④在射线AC上取一点E,画线段BE,使其长度表示点B到AC的距离;
(2)在(1)所画图中,
①BD与BE的位置关系为 ;
②线段BE与BC的大小关系为BE BC(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β |=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
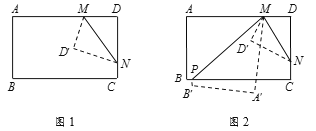
(1)若∠A=80°,则∠A的半余角的度数为 ;
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题引入】
已知:如图BE、CF是ΔABC的中线,BE、CF相交于G。求证: ![]()
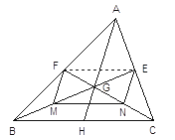
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF=![]() BC
BC
∴![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点 (填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是 四边形。
②当![]() 的值为 时,四边形EFMN 是矩形。
的值为 时,四边形EFMN 是矩形。
③当![]() 的值为 时,四边形EFMN 是菱形。
的值为 时,四边形EFMN 是菱形。
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积![]() =_________
=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
由于发展时间早、发展速度快,经过20多年大规模的高速开发建设,北京四环内,甚至五环内可供开发建设的土地资源越来越稀缺,更多的土地供应将集中在五环外,甚至六环外的远郊区县.
据中国经济网2017年2月报道,来自某市场研究院的最新统计,2016年,剔除了保障房后,在北京新建商品住宅交易量整体上涨之时,北京各区域的新建商品住宅交易量则是有涨有跌![]() 其中,昌平、通州、海淀、朝阳、西城、东城六区下跌,跌幅最大的为朝阳区,新建商品住宅成交量比2015年下降了
其中,昌平、通州、海淀、朝阳、西城、东城六区下跌,跌幅最大的为朝阳区,新建商品住宅成交量比2015年下降了![]() 而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨,涨幅最大的为顺义区,比2015年上涨了
而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨,涨幅最大的为顺义区,比2015年上涨了![]() 另外,从环线成交量的占比数据上,同样可以看出成交日趋郊区化的趋势
另外,从环线成交量的占比数据上,同样可以看出成交日趋郊区化的趋势![]() 根据统计,2008年到2016年,北京全市成交的新建商品住宅中,二环以内的占比逐步从
根据统计,2008年到2016年,北京全市成交的新建商品住宅中,二环以内的占比逐步从![]() 下降到了
下降到了![]() ;二、三环之间的占比从
;二、三环之间的占比从![]() 下降到了
下降到了![]() ;三、四环之间的占比从
;三、四环之间的占比从![]() 下降到了
下降到了![]() ;四、五环之间的占比从
;四、五环之间的占比从![]() 下降到了
下降到了![]() 也就是说,整体成交中位于五环之内的新房占比,从2008年的
也就是说,整体成交中位于五环之内的新房占比,从2008年的![]() 下降到了2016年的
下降到了2016年的![]() ,下滑趋势非常明显
,下滑趋势非常明显![]() 由此可见,新房市场的远郊化是北京房地产市场发展的大势所趋
由此可见,新房市场的远郊化是北京房地产市场发展的大势所趋![]() 注:占比,指在总数中所占的比重,常用百分比表示
注:占比,指在总数中所占的比重,常用百分比表示![]()
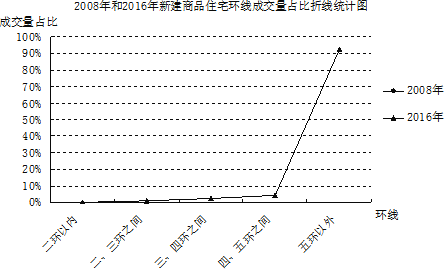
根据以上材料解答下列问题:
![]() 补全折线统计图;
补全折线统计图;
![]() 根据材料提供的信息,预估2017年位于北京市五环之内新建商品住宅成交量占比约______ ,你的预估理由是______ .
根据材料提供的信息,预估2017年位于北京市五环之内新建商品住宅成交量占比约______ ,你的预估理由是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.有且只有一条直线与已知直线垂直;
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线距离;
C.互相垂直的两条线段一定相交;
D.直线![]() 外一点
外一点![]() 与直线
与直线![]() 上各点连接而成的所有线段中,最短线段的长度是
上各点连接而成的所有线段中,最短线段的长度是![]() ,则点
,则点![]() 到直线
到直线![]() 的距离是
的距离是![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过直线![]() 上点
上点![]() 作
作![]() 的垂线
的垂线![]() ,三角尺的一条直角边
,三角尺的一条直角边![]() 从与
从与![]() 重合的位置开始,绕点
重合的位置开始,绕点![]() 按逆时针方向旋转至与
按逆时针方向旋转至与![]() 重合时停止,在旋转过程中,设
重合时停止,在旋转过程中,设![]() 的度数为
的度数为![]() ,作
,作![]() 的平分线
的平分线![]() .
.
(1)当![]() 在
在![]() 的内部时,
的内部时,![]() 的余角是___________;(填写所有符合条件的角)
的余角是___________;(填写所有符合条件的角)
(2)在旋转过程中,若![]() ,求
,求![]() 的值;
的值;
(3)在旋转过程中,作![]() 的平分线
的平分线![]() 的度数是否会随着
的度数是否会随着![]() 的变化而变化?若不变,直接写出
的变化而变化?若不变,直接写出![]() 的度数;若变化,试用含有
的度数;若变化,试用含有![]() 的式子表示
的式子表示![]() 的度数.
的度数.
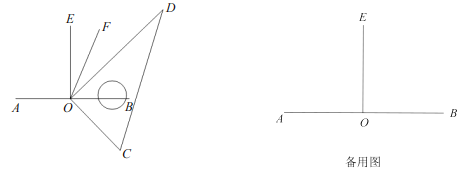
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com