
【题目】如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β |=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
(1)若∠A=80°,则∠A的半余角的度数为 ;
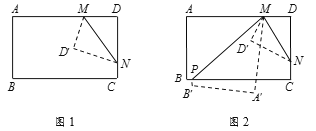
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
【答案】(1)35°或125°;(2)45°或75°;(3)10°或130°.
【解析】
(1)设∠A的半余角的度数为x°,根据半余角的定义列方程求解即可;
(2)设∠DMN为x°.根据折叠的性质和半余角的定义解答即可;
(3)分两种情况讨论:①当∠DMN=45°时,∠DMD'=90°,∠AMP=50°,∠DMA'=80°,根据∠A′MD′=∠DMD'-∠DMA'计算即可.
②当∠DMN=75°时,∠DMD'=150°,∠AMP=80°,∠DMA'=20°,根据∠A′MD′=∠DMD'-∠DMA'计算即可.
(1)设∠A的半余角的度数为x°,根据题意得:
|80°-x|=45°
80°-x=±45°
∴x=80°±45°,
∴x=35°或125°.
(2)设∠DMN为x°,根据折叠的性质得到∠D'MN=∠DMN=x°.
∴∠AMD'=180°-2x.
∵∠AMD′与∠DMN互为“半余角”,
∴|180°-2x-x|=45°,
∴|180°-3x|=45°,
∴180°-3x=45°或180°-3x=-45°,
解得:x=45°或x=75°.
(3)分两种情况讨论:①当∠DMN=45°时,∠D'MN=45°,
∴∠DMD'=90°,∠AMP=∠A'MP=45°+5°=50°,
∴∠DMA'=180°-2∠AMP=80°,
∴∠A′MD′=∠DMD'-∠DMA'=90°-80°=10°.
②当∠DMN=75°时,∠D'MN=75°,
∴∠DMD'=150°,∠AMP=∠A'MP=75°+5°=80°,
∴∠DMA'=180°-2∠AMP=20°,
∴∠A′MD′=∠DMD'-∠DMA'=150°-20°=130°.
综上所述:∠A′MD′的度数为10°或130°.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:![]() ,且
,且![]() 、
、![]() 、
、![]() 分别是点A. B. C在数轴上对应的数.
分别是点A. B. C在数轴上对应的数.

(1)写出![]() =___;
=___;![]() =___;
=___;![]() =___.
=___.
(2)若甲、乙、丙三个动点分别从A.B.C三点同时出发沿数轴负方向运动,它们的速度分别是1、2、4,(单位/秒),运行![]() 秒后,甲、乙、丙三个动点对应的位置分别为:
秒后,甲、乙、丙三个动点对应的位置分别为:![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求式子
时,求式子![]() 的值.
的值.
(3)若甲、乙、丙三个动点分别从A,B,C三点同时出发沿数轴正方向运动,它们的速度分别是1,2,4(单位/秒),运动多长时间后,乙与甲、丙等距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织360名师生外出活动,计划租用甲、乙两种型号的客车;经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)已知师生行李打包后共有164件,若租用10辆甲、乙两种型号的客车,请你帮助设计出该校所有可行的租车方案;
(2)若师生行李打包后共有m件,且170 < m ≤ 184,如果所租车辆刚好把所有师生和行李载走(每辆车均以最多承载量载满),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() 的度数是
的度数是![]() 的度数的k倍,则规定
的度数的k倍,则规定![]() 是
是![]() 的k倍角.
的k倍角.
(1)若∠M=21°17',则∠M的5倍角的度数为 ;
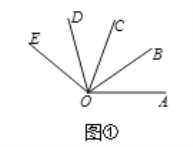
(2)如图1,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=∠COE,请直接写出图中∠AOB的所有3倍角;
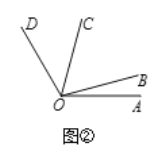
(3)如图2,若∠AOC是∠AOB的5倍角,∠COD是∠AOB的3倍角,且∠AOC和∠BOD互为补角,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.

(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)当t为何值时,△PQF为等腰三角形?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
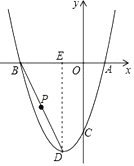
【题目】如图,已知抛物线y = x2 + bx + c的图象经过点A(l ,0) ,B(﹣3 ,0) ,与y轴交于点C ,抛物线的顶点为D ,对称轴与x轴相交于点E ,连接BD .
(1)求抛物线的解析式 .
(2)若点P在直线BD上,当PE = PC时,求点P的坐标 .
(3)在(2)的条件下,作PF⊥x轴于F ,点M为x轴上一动点 ,N为直线PF上一动点 ,G为抛物线上一动点,当以点F ,N ,G ,M 四点为顶点的四边形为正方形时,求点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
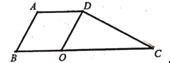
【题目】如图,四边形ABCD中AD∥BC, ∠B=60°,AB=AD=BO=4cm,OC=8cm, 点M从B点出发,按从B→A→D→C的方向,沿四边形BADC的边以1cm/s的速度作匀速运动,运动到点C即停止.若运动的时间为t,△MOD的面积为y,则y关于t的函数图象大约是( )
A. B.
B.
C.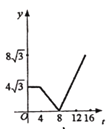 D.
D.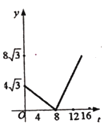
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com