
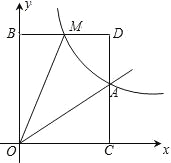
【题目】已知,如图,正比例函数y=ax的图象与反比例函数y=![]() 的图象交于点A(3,2).
的图象交于点A(3,2).
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象直接写出在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,试说明BM=DM.
【答案】(1)正比例函数表达式为y=![]() x,反比例函数表达式为y=
x,反比例函数表达式为y=![]() ;(2)当0<x<3时;(3)证明参见解析.
;(2)当0<x<3时;(3)证明参见解析.
【解析】
试题分析:(1)把A点坐标分别代入两函数解析式可求得a和k的值,可求得两函数的解析式;(2)由反比例函数的图象在正比例函数图象的上方可求得对应的x的取值范围;(3)用M点的坐标可表示矩形OCDB的面积和△OBM的面积,从而可表示出四边形OADM的面积,可得到方程,可求得M点的坐标,从而可证明结论.
试题解析:(1)∵正比例函数y=ax的图象与反比例函数y=![]() 的图象交于点A(3,2),∴2=3a,2=
的图象交于点A(3,2),∴2=3a,2=![]() ,解得a=
,解得a=![]() ,k=6,∴正比例函数表达式为y=
,k=6,∴正比例函数表达式为y=![]() x,反比例函数表达式为y=
x,反比例函数表达式为y=![]() ;(2)由图象可知当两函数图象在直线CD的左侧时,反比例函数的图象在正比例函数图象的上方,∵A(3,2),∴当0<x<3时,反比例函数的值大于正比例函数的值;(3)由题意可知四边形OCDB为矩形,∵M(m,n),A(3,2),∴OB=n,BM=m,OC=3,AC=2,∴S矩形OCBD=OCOB=3n,S△OBM=
;(2)由图象可知当两函数图象在直线CD的左侧时,反比例函数的图象在正比例函数图象的上方,∵A(3,2),∴当0<x<3时,反比例函数的值大于正比例函数的值;(3)由题意可知四边形OCDB为矩形,∵M(m,n),A(3,2),∴OB=n,BM=m,OC=3,AC=2,∴S矩形OCBD=OCOB=3n,S△OBM=![]() OBBM=
OBBM=![]() mn,S△OCA=
mn,S△OCA=![]() OCAC=3,∴S四边形OADM=S矩形OCBD﹣S△OBM﹣S△OCA=3n﹣
OCAC=3,∴S四边形OADM=S矩形OCBD﹣S△OBM﹣S△OCA=3n﹣![]() mn﹣3,当四边形OADM的面积为6时,则有3n﹣
mn﹣3,当四边形OADM的面积为6时,则有3n﹣![]() mn﹣3=6,又∵M点在反比例函数图象上,∴mn=6,∴3n=12,解得n=4,则m=
mn﹣3=6,又∵M点在反比例函数图象上,∴mn=6,∴3n=12,解得n=4,则m=![]() ,∵BD=OC=3,∴M为BD中点,∴BM=DM.
,∵BD=OC=3,∴M为BD中点,∴BM=DM.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】为帮助灾区人民重建家园,某校学生积极捐款.已知第一次捐款总额为9000元,第二次捐款总额为12000元,两次人均捐款额相等,但第二次捐款人数比第一次多50人.求该校第二次捐款的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“迎新年,庆元旦”期间,某商场推出A、B、C、D四种不同类型礼盒共1000盒进行销售,在图1中是各类型礼盒所占数的百分比,已知四类礼盒一共已经销售了50%,各类礼盒的销售数量如图2所示: 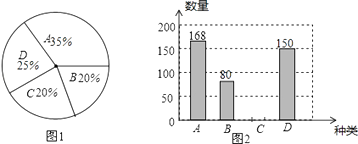
(1)商场中的D类礼盒有盒.
(2)请在图1扇形统计图中,求出A部分所对应的圆心角等于度.
(3)请将图2的统计图补充完整.
(4)通过计算得出类礼盒销售情况最好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数 y=﹣3x+1,下列结论正确的是( )
A. 它的图象必经过点(﹣1,3) B. 它的图象经过第一、二、三象限
C. y的值随x值的增大而增大 D. 当x>1时,y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,线段AB=6cm,C点从P点出发以1cm/s的速度沿AB向左运动,D点从B出发以2cm/s的速度沿AB向左运动(C在线段AP上,D在线段BP上) 
(1)若C,D运动到任意时刻都有PD=2AC,求出P在AB上的位置;
(2)在(1)的条件下,Q是直线AB上一点,若AQ﹣BQ=PQ,求PQ的值;
(3)在(1)的条件下,若C,D运动了一段时间后恰有AB=2CD,这时点C停止运动,点继续在线段PB上运动,M,N分别是CD,PD的中点,求出MN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
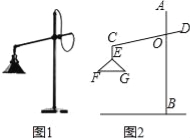
【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com