
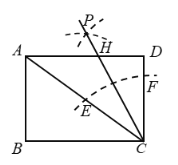
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() .以点
.以点![]() 为圆心,以任意长为半径作弧,交
为圆心,以任意长为半径作弧,交![]() ,
,![]() 分别于点
分别于点![]() ,
,![]() :分别以点
:分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 长为半径作弧,两弧相交于点
长为半径作弧,两弧相交于点![]() :作射线
:作射线![]() ,交
,交![]() 于点
于点![]() .则
.则![]() 的面积为_________.
的面积为_________.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中数学 来源: 题型:
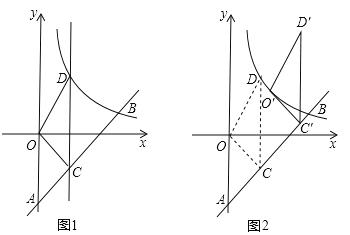
【题目】(2016江苏省镇江市) (2016镇江)如图1,一次函数y=kx﹣3(k≠0)的图象与y轴交于点A,与反比例函数![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上的动点(于点A、B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求△OCD面积的最大值;
(3)将(2)中面积取得最大值的△OCD沿射线AB方向平移一定的距离,得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上(如图2),则点D′的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,在![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上任意一点,
上任意一点,![]() 是等边三角形,且点
是等边三角形,且点![]() 在
在![]() 的内部,连接
的内部,连接![]() .探究线段
.探究线段![]() 与
与![]() 之间的数量关系.
之间的数量关系.
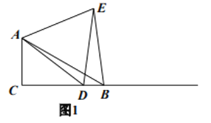
请你完成下列探究过程:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
![]() 当点
当点![]() 与点
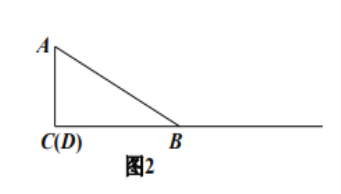
与点![]() 重合时(如图2),请你补全图形.由
重合时(如图2),请你补全图形.由![]() 的度数为_______________,点
的度数为_______________,点![]() 落在_______________,容易得出
落在_______________,容易得出![]() 与
与![]() 之间的数量关系为_______________
之间的数量关系为_______________
![]() 当
当![]() 是
是![]() 的平分线时,判断
的平分线时,判断![]() 与
与![]() 之间的数量关系并证明
之间的数量关系并证明
![]() 当点
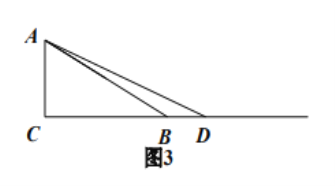
当点![]() 在如图3的位置时,请你画出图形,研究
在如图3的位置时,请你画出图形,研究![]() 三点是否在以
三点是否在以![]() 为圆心的同一个圆上,写出你的猜想并加以证明.
为圆心的同一个圆上,写出你的猜想并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
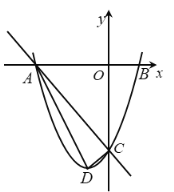
【题目】如图,顶点为![]() 的抛物线
的抛物线![]() 与交
与交![]() 轴分别于点
轴分别于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),与交
的左侧),与交![]() 轴交于点
轴交于点![]() .已知直线
.已知直线![]() 的解析式为
的解析式为![]() .
.
(1)求抛物线的解析式:
(2)若以点![]() 为圆心的圆与
为圆心的圆与![]() 相切,求
相切,求![]() 的半径;
的半径;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似?如果存在,请求出点
相似?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
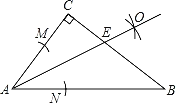
【题目】如图所示,在Rt△ABC中,∠C=90°,按以下步骤作图:
①以点A为圆心,以小于AC的长为半径作弧,分别交AC、AB于点M,N;
②分别以点M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点O;
MN的长为半径作弧,两弧相交于点O;
③作射线OA,交BC于点E,若CE=6,BE=10.
则AB的长为( )
A.11B.12C.18D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
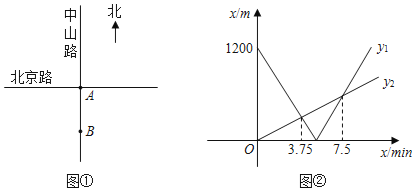
【题目】如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点![]() .甲从中山路上点
.甲从中山路上点![]() 出发,骑车向北匀速直行;与此同时,乙从点
出发,骑车向北匀速直行;与此同时,乙从点![]() 出发,沿北京路步行向东匀速直行.设出发
出发,沿北京路步行向东匀速直行.设出发![]() 时,甲、乙两人与点
时,甲、乙两人与点![]() 的距离分别为
的距离分别为![]() 、
、![]() .已知
.已知![]() 、
、![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
(1)求甲、乙两人的速度;
(2)当![]() 取何值时,甲、乙两人之间的距离最短?
取何值时,甲、乙两人之间的距离最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,点E,F分别是BC,AD的中点.
,点E,F分别是BC,AD的中点.
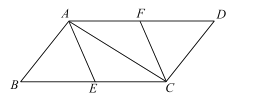
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形
满足什么数量关系时,四边形![]() 是正方形?请证明.
是正方形?请证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com