如图.在正方形ABCD中∠DAE=25°.AE交对角线BD于E点.那么∠BEC等于( )A．45°B．60°C．70°D．75° 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

15．

如图，在正方形ABCD中∠DAE=25°，AE交对角线BD于E点，那么∠BEC等于（　　）

A．

45°

B．

60°

C．

70°

D．

75°

分析首先证明△AED≌△CED，即可证明∠ECD=∠DAE=25°，从而求得∠BEC，再根据三角形内角和定理即可求解．

解答解：在△AED和△CED中，
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDE}\\{DE=DE}\end{array}\right.$，
∴△AED≌△CED，
∴∠ECD=∠DAE=25°，
又∵在△DEC中，∠CDE=45°，
∴∠CED=180°-25°-45°=110°，
∴∠BEC=180°-110°=70°．
故选：C．

点评此题主要考查了正方形的性质，正确理解，证明△AED≌△CED是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

5．

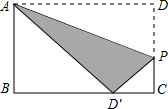如图，矩形ABCD中，AB=8，BC=10，点P在矩形的边DC上由点D向点C运动，沿直线AP翻折三角形ADP，使点D恰好落在BC边上．求DP的长和三角形ADP与矩形重叠（阴影）部分的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

6．若$\frac{3a+1}{（a+3）（a-1）}$=$\frac{m}{a+3}$+$\frac{n}{a-1}$，则（　　）

A．

m=-3，n=1

B．

m=3，n=-1

C．

m=3，n=1

D．

m=2，n=1

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．若x+y=3，且（x+2）（y+2）=12．
（1）求xy的值；
（2）求x²-xy+y²的值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．解方程组：
（1）$\left\{\begin{array}{l}{2x+5y=13}\\{3x-5y=7}\end{array}\right.$
（2）$\left\{\begin{array}{l}{\frac{x}{4}+\frac{y}{3}=3}\\{3x-2（y-1）=11}\end{array}\right.$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

20．若关于x的一元二次方程kx²-2x-1=0有两个不相等的实数根，则k的取值范围是（　　）

A．

k＞-1

B．

k＞-1且k≠0

C．

k＜1

D．

k＜1且k≠0

查看答案和解析>>