
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.
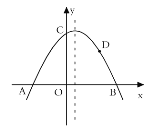
(1)求抛物线的表达式;
(2)点![]() 是抛物线上一点.
是抛物线上一点.
①在抛物线的对称轴上,求作一点![]() ,使得
,使得![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标;
的坐标;
②连接![]() 并延长,过抛物线上一点
并延长,过抛物线上一点![]() (点
(点![]() 不与点
不与点![]() 重合)作
重合)作![]() 轴,垂足为
轴,垂足为![]() ,与射线
,与射线![]() 交于点
交于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①连接
;(2)①连接![]() 交抛物线对称轴于点
交抛物线对称轴于点![]() ,则点
,则点![]() 即为所求,点
即为所求,点![]() 的坐标为
的坐标为![]() ;②存在;点
;②存在;点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)由![]() ,
,![]() 得到A(-2,0),C(3,0),即可写出抛物线的交点式.
得到A(-2,0),C(3,0),即可写出抛物线的交点式.
(2)①因为![]() 关于对称轴对称,所以
关于对称轴对称,所以![]() ,由两点之间线段最短,知连接
,由两点之间线段最短,知连接![]() 交抛物线对称轴于点
交抛物线对称轴于点![]() ,则点
,则点![]() 即为所求,先用待定系数法求出
即为所求,先用待定系数法求出![]() 解析式,将对称轴代入得到
解析式,将对称轴代入得到![]() 点坐标.
点坐标.
②设点![]() ,根据抛物线的解析式、直线
,根据抛物线的解析式、直线![]() 的解析式,写出Q、M的坐标,分当
的解析式,写出Q、M的坐标,分当![]() 在
在![]() 上方、下方两种情况,列关于m的方程,解出并取大于-2的解,即可写出
上方、下方两种情况,列关于m的方程,解出并取大于-2的解,即可写出![]() 的坐标.
的坐标.
(1)∵![]() ,
,![]() ,
,
结合图象,得A(-2,0),C(3,0),
∴抛物线![]() 可表示为:
可表示为:![]() ,
,
∴抛物线的表达式为![]() ;
;
(2)①∵![]() 关于对称轴对称,
关于对称轴对称,
∴![]() ,
,
∴连接![]() 交抛物线对称轴于点
交抛物线对称轴于点![]() ,则点
,则点![]() 即为所求.
即为所求.
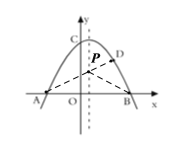
将点![]() ,
,![]() 的坐标代入一次函数表达式
的坐标代入一次函数表达式![]() ,
,
得直线![]() 的函数表达式为
的函数表达式为![]() .
.
抛物线的对称轴为直线![]() ,
,
当![]() 时,
时,![]() ,
,
故点![]() 的坐标为
的坐标为![]() ;
;
②存在;设点![]() ,则
,则![]() ,
,![]() .
.
当![]() 在
在![]() 上方时,
上方时,
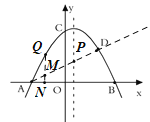
![]() ,
,![]() ,
,![]() ,解得
,解得![]() (舍)或
(舍)或![]() ;
;
当![]() 在
在![]() 下方时,
下方时,
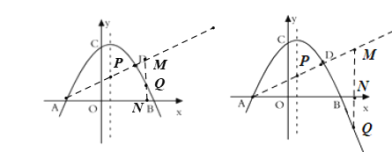
![]() ,
,![]() ,
,![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
综上所述,![]() 的值为
的值为![]() 或5,
或5,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
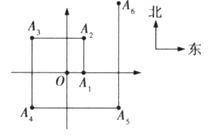
【题目】如图,一个机器人从点O出发,向正东方向走3m到达点![]() ,再向正北方向走6m到达点
,再向正北方向走6m到达点![]() ,再向正西方向走9m到达点
,再向正西方向走9m到达点![]() ,再向正南方向走12m到达点
,再向正南方向走12m到达点![]() ,再向正东方向走15m到达点
,再向正东方向走15m到达点![]() ,按如此规律走下去,当机器人走到点
,按如此规律走下去,当机器人走到点![]() 时,点
时,点![]() 的坐标是________.
的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是一张等腰直角三角形彩色纸,AC=BC,将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.若用这4张纸条刚好可以为一幅正方形美术作品镶边(纸条不重叠),如图2,则正方形美术作品与镶边后的作品的面积之比为_____.
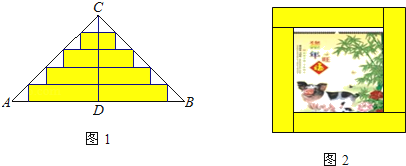
查看答案和解析>>
科目:初中数学 来源: 题型:
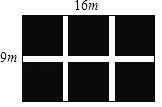
【题目】如图,某小区在一块长为16m,宽为9m的矩形空地上新修三条宽度相同的小路,其中一条和矩形的一边平行,另外两条和矩形的另一边平行,空地剩下的部分种植花草,使得花草区域占地面积为120m2.设小路的宽度为xm,则下列方程:
①(16﹣2x)(9﹣x)=120
②16×9﹣9×2x﹣(16﹣2x)x=120
③16×9﹣9×2x﹣16x+x2=120,
其中正确的是( )
A.①B.②C.①②D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=![]() ,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )
,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )

A. 2 ![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
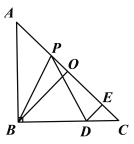
【题目】如图所示,在等腰直角三角形ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为点E,求证:PE=BO
查看答案和解析>>
科目:初中数学 来源: 题型:
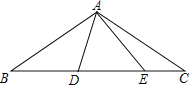
【题目】如图,在△ABC中,AB=AC=2![]() ,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为________.
,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com