
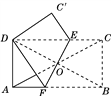
【题目】如图,在矩形纸片ABCD中,AC,BD相交于点O,AD∶AB=1∶2,AC=![]() ,将纸片折叠使点B与点D重合,求折叠后纸片重合部分的面积.
,将纸片折叠使点B与点D重合,求折叠后纸片重合部分的面积.
 (
(
【答案】折叠后纸片重合部分的面积为![]() .
.
【解析】试题分析:设AD=x,则AB=2x,根据勾股定理求得x的值,根据已知条件证明△ODE≌△OBF,根据全等三角形的性质可得DE=BF,由折叠可知BF=DF,设DE=DF=BF=y,则AF=2-y,在Rt△ADF中,由勾股定理列出方程求得y的值,即可求得折叠后纸片重合部分的面积.
试题解析:
设AD=x,则AB=2x.在矩形ABCD中,AB=CD.
在Rt△ADC中,AC=![]() ,AD2+CD2=AC2,
,AD2+CD2=AC2,
∴x2+(2x)2=(![]() )2.
)2.
解得x=1(负根舍去),即AD=1,AB=2.
在矩形ABCD中,OD=OB,ED∥BF,
∴∠ODE=∠OBF,∠OED=∠OFB,
∴△ODE≌△OBF(AAS),∴DE=BF.
由折叠,得BF=DF,∴DE=DF=BF.
设DE=DF=BF=y,则AF=2-y.
在Rt△ADF中,由勾股定理,得12+(2-y)2=y2.
解得y=![]() ,即DE=BF=
,即DE=BF=![]() .
.
故S△DEF=![]() DE·AD=
DE·AD=![]() ×
×![]() ×1=
×1=![]() .
.
∴折叠后纸片重合部分的面积为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=![]() ,求AD和AB的长.
,求AD和AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)( ![]() )﹣1+(π﹣3)0+(﹣2)﹣2+|(﹣2)3|
)﹣1+(π﹣3)0+(﹣2)﹣2+|(﹣2)3|
(2)(9x3y﹣12xy3+3xy2)÷(﹣3xy)﹣(2y+x)(2y﹣x),其中x=1,y=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
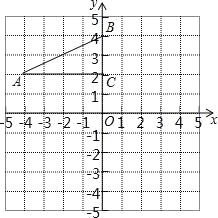
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列线段中,能成比例的是( )
A. 3cm、6cm、8cm、9cmB. 3cm、5cm、6cm、9cm
C. 3cm、6cm、7cm、9cmD. 3cm、6cm、9cm、18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 过原点的直线都是正比例函数 B. 正比例函数图象经过原点
C. y=kx是正比例函数 D. y=3+x是正比例函数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类且定价为15元的图书,书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠,学校如果多买12本,则可以享受优惠且所花钱数与原来相同,问学校获奖的同学有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com