
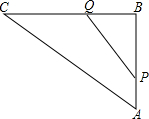
 如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动.
如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动. 如图,∵在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,
如图,∵在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,| AC2-BC2 |
| BQ2+BP2 |
| (1.5×20)2+(60-20)2 |
| 50 |
| 1+1.5 |


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
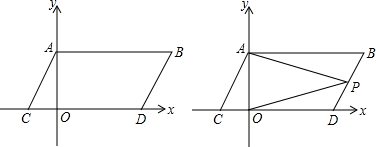
| ∠BAP+∠DOP |
| ∠APO |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
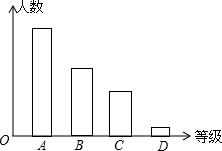 吉安市某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
吉安市某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:
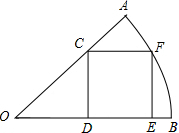 如图,在半径为
如图,在半径为| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com